Nếu hôm nay là Chủ nhật thì ngày mai là Thứ Hai là điều chắc chắn. Chắc chắn mặt trời sẽ mọc ở hướng đông. Ngoài ra, bạn không thể cao hơn hươu cao cổ được. Đối với một số sự kiện, chúng ta chắc chắn về kết quả. Nhưng hãy nghĩ đến tình huống bạn đang cạnh tranh với tám vận động viên khác để giành chiến thắng trong cuộc đua. Bạn có thể thắng cuộc đua nhưng điều đó không chắc chắn. Khi bạn mua vé số, bạn có thể thắng. Nhưng vì có hàng vạn người đã mua vé số cho cùng một loại vé số nên khả năng bạn trúng giải là rất ít.
Cơ hội xảy ra một sự kiện khi được đo lường một cách định lượng được gọi là xác suất. Xác suất sử dụng các con số để đo lường khả năng xảy ra một kết quả. Xác suất của một kết quả có thể được hiển thị bằng thang đo dưới đây:
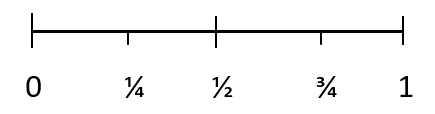
Tất cả xác suất đều có giá trị từ 0 đến 1. Xác suất của một kết quả không thể xảy ra là 0. Và xác suất của một kết quả nhất định là 1. 1/4 đại diện cho một sự kiện khó có thể xảy ra, 1/2 đại diện cho khả năng xảy ra chẵn của một kết quả nào đó. sự kiện và 3/4 đại diện cho một sự kiện có khả năng xảy ra.
Hãy đánh dấu từng kết quả này theo thang xác suất:
Xác suất xảy ra sự kiện E, ký hiệu là P(E), được định nghĩa là
\(P(E) =\frac{\textrm{Số kết quả thuận lợi}}{\textrm{Tổng số kết quả có thể xảy ra}} = \frac{e}{n}\)
trong đó kết quả là kết quả của thí nghiệm. Một kết quả thuận lợi là sự kiện đó có xác suất xảy ra mà chúng ta muốn xác định.
Hãy cùng tìm hiểu xác suất qua một vài ví dụ:
1) Nếu một quân bài được rút ra từ một bộ bài được xáo trộn kỹ gồm 52 quân bài thì xác suất để rút được quân hậu là bao nhiêu?
Giải: Tổng số kết quả có thể xảy ra = 52
Có 4 quân hậu trong bộ bài 52 lá và bất kỳ quân hậu nào cũng có thể được rút ra.
Do đó, số kết quả thuận lợi = 4
Xác suất để rút được quân hậu là \(\frac{4}{52} = \frac{1}{13}\)
2) Xác suất để có được số chẵn khi tung xúc xắc là bao nhiêu?
Giải: Tổng số kết quả = 6
Tổng số kết quả thuận lợi = 3 (các số chẵn là 2, 4 và 6)
Do đó, xác suất để nhận được số chẵn là \(\frac{3}{6} = \frac{1}{2}\)