Primer lesson: الانحدار الإحصائي

سوف تتعلم:

ما هو الانحدار الإحصائي؟
معادلة الانحدار الخطي واشتقاقها
استخدام تحليل الانحدار

تحليل الانحدار هو طريقة لربط المتغيرات ببعضها البعض. المتغيرات هي ببساطة أجزاء من المعلومات التي جمعناها. باستخدام تحليل الانحدار ، يمكننا العثور على أنماط في بياناتنا. يسمح لنا بعمل تنبؤات بناءً على بياناتنا. الانحدار الإحصائي هو أسلوب يستخدم لتحديد كيفية تأثر المتغير التابع بواحد أو أكثر من المتغيرات المستقلة. من الناحية الرياضية ، يجيب الانحدار الإحصائي على السؤال التالي: ماذا سيكون التأثير على قيمة Y (المتغير التابع) إذا تغيرت قيمة X (المتغير المستقل)؟

على سبيل المثال - نريد معرفة العلاقة بين عمر وسعر السيارات المستعملة التي تم بيعها العام الماضي بواسطة تاجر سيارات. سنرى علاقة سلبية بين هذين المتغيرين. كلما زاد عمر السيارة ، تنخفض الأسعار. في هذا المثال ، يعتبر عمر السيارة وسعر السيارة متغيرين. سعر السيارة يعتمد على عمر السيارة. ما نريد إيجاده هو المعادلة التي تناسب البيانات التي لدينا. يُطلق على نموذج تحليل الانحدار البسيط للغاية الذي يمكننا استخدامه لمثالنا النموذج الخطي ، والذي يستخدم معادلة خطية بسيطة لتلائم البيانات. تعطيك المعادلات الخطية عند رسمها خطًا مستقيمًا.

معادلة الانحدار الخطي أو التي يتم التعرف عليها أيضًا على أنها صيغة المنحدر لها الشكل Y = a + bX ، حيث Y هو المتغير التابع (هذا هو المتغير الذي يذهب على المحور Y) ، X هو المتغير المستقل (أي أنه مرسوم على المحور السيني) ، ب هو ميل الخط و أ هو تقاطع ص (قيمة ص عندما س = 0).

ميل الخط هو القيمة التي تصف معدل التغيير بين المتغيرات المستقلة والتابعة. يخبرنا المنحدر كيف يتغير المتغير التابع ( ص ) لكل وحدة زيادة في المتغير المستقل ( س ) ، في المتوسط. يتم استخدام تقاطع ص لوصف المتغير التابع عندما يساوي المتغير المستقل صفرًا.

\(a = \frac{(\Sigma y)(\Sigma x^2) - (\Sigma x) (\Sigma xy)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

\(b = \frac{n(\Sigma xy) - (\Sigma x) (\Sigma y)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

يُظهر b> 0 علاقة إيجابية بين المتغيرين.

يمكنك أيضًا استخدام أي برنامج إحصائي مثل excel للحصول على معادلة الانحدار الخطي ، لرسم المخطط المبعثر ، ورسم خط الانحدار.

كيف يعمل تحليل الانحدار؟
يتكون الانحدار الخطي من إيجاد أفضل خط مستقيم عبر النقاط. حدد متغيرًا تابعًا تفترض أنه يتأثر بمتغير واحد أو عدة متغيرات مستقلة. اجمع مجموعة البيانات لهذه المتغيرات.
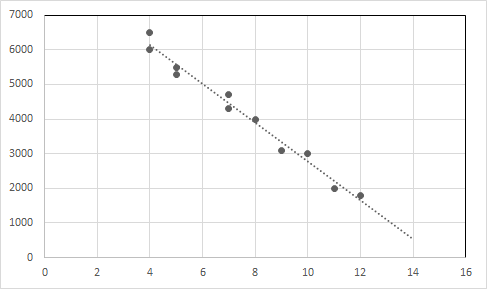
مثال 1: دعنا ننظر في البيانات أدناه لبيع السيارات المستعملة.

عمر السيارة (بالسنوات)	السعر (بالدولار)
4	6500
4	6000
5	5500
5	5300
7	4700
7	4300
8	4000
9	3100
10	3000
11	2000
12	1800

بالنظر إلى البيانات يمكننا القول أن سعر السيارة ينخفض مع زيادة عمر السيارة.

صيغة خط الانحدار هي Y = a + bX ، واشتق a و b باستخدام الصيغ أدناه

\(a = \frac{(\Sigma y)(\Sigma x^2) - (\Sigma x) (\Sigma xy)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

\(b = \frac{n(\Sigma xy) - (\Sigma x) (\Sigma y)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

معادلة الانحدار الخطي لهذه العلاقة هي Y = -557.62125 X + 8356.81293

ارسم نقاط البيانات وخط الانحدار في رسم بياني.

المحور السيني: العمر ، المحور الصادي: السعر

مثال 2: جون سباك. يتقاضى 25 دولارًا كرسوم زيارة و 35 دولارًا كرسوم عمل بالساعة. المعادلة الخطية التي تعبر عن المبلغ الإجمالي للأموال التي يكسبها جون لكل زيارة هي y = 25 + 35x.

لماذا تحليل الانحدار؟

يمكن استخدام الانحدار لتحديد قوة تأثير المتغير (المتغيرات) المستقلة على متغير تابع. مثال - ما هي قوة العلاقة بين الجرعة والتأثير ، والإنفاق على المبيعات والتسويق ، أو العمر والدخل.
يمكن استخدامه للتنبؤ بآثار أو تأثير التغييرات. أي أن تحليل الانحدار يساعدنا على فهم مدى تغير المتغير التابع مع تغيير واحد أو أكثر من المتغيرات المستقلة. مثال - ما مقدار دخل المبيعات الإضافي الذي أحصل عليه مقابل كل 1000 دولار إضافية يتم إنفاقها على التسويق؟
يتنبأ تحليل الانحدار بالاتجاهات والقيم المستقبلية. يمكن استخدام تحليل الانحدار للحصول على تقديرات النقاط. على سبيل المثال ، كم سيكون سعر الذهب في 6 أشهر؟

الانحدار الإحصائي

\(a = \frac{(\Sigma y)(\Sigma x^2) - (\Sigma x) (\Sigma xy)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

\(b = \frac{n(\Sigma xy) - (\Sigma x) (\Sigma y)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

\(a = \frac{(\Sigma y)(\Sigma x^2) - (\Sigma x) (\Sigma xy)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

\(b = \frac{n(\Sigma xy) - (\Sigma x) (\Sigma y)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

Download Primer to continue