তুমি শিখবে:
রিগ্রেশন বিশ্লেষণ হল ভেরিয়েবলকে একে অপরের সাথে সম্পর্কিত করার একটি উপায়। ভেরিয়েবল হল শুধুমাত্র আমরা সংগ্রহ করা তথ্যের বিট। রিগ্রেশন বিশ্লেষণ ব্যবহার করে, আমরা আমাদের ডেটাতে নিদর্শন খুঁজে পেতে পারি। এটি আমাদের ডেটার উপর ভিত্তি করে ভবিষ্যদ্বাণী করতে দেয়। পরিসংখ্যানগত রিগ্রেশন হল একটি কৌশল যা নির্ভরশীল ভেরিয়েবল কিভাবে এক বা একাধিক স্বাধীন ভেরিয়েবল দ্বারা প্রভাবিত হয় তা নির্ধারণ করতে ব্যবহৃত হয়। গাণিতিক পরিভাষায় পরিসংখ্যানগত রিগ্রেশন প্রশ্নের উত্তর দেয়: X (স্বতন্ত্র চলক) এর মান পরিবর্তন করা হলে Y (নির্ভরশীল চলক) মানের উপর কী প্রভাব পড়বে?
যেমন- আমরা একজন গাড়ি ব্যবসায়ীর দ্বারা গত বছর বিক্রি করা ব্যবহৃত গাড়ির বয়স ও দামের মধ্যে সম্পর্ক খুঁজে বের করতে চাই। আমরা এই দুটি ভেরিয়েবলের মধ্যে একটি নেতিবাচক সম্পর্ক দেখতে পাব। গাড়ির বয়স বাড়ার সাথে সাথে দাম কমতে থাকে। এই উদাহরণে, গাড়ির বয়স এবং গাড়ির দাম দুটি পরিবর্তনশীল। গাড়ির দাম গাড়ির বয়সের উপর নির্ভর করে। আমরা যা খুঁজতে চাই তা হল এমন একটি সমীকরণ যা আমাদের কাছে থাকা ডেটার সাথে সবচেয়ে ভাল ফিট করে। একটি খুব সাধারণ রিগ্রেশন বিশ্লেষণ মডেল যা আমরা আমাদের উদাহরণের জন্য ব্যবহার করতে পারি তাকে রৈখিক মডেল বলা হয়, যা ডেটা ফিট করার জন্য একটি সাধারণ রৈখিক সমীকরণ ব্যবহার করে। গ্রাফ করা হলে রৈখিক সমীকরণগুলি আপনাকে একটি সরল রেখা দেয়।
রৈখিক রিগ্রেশন সমীকরণ বা ঢাল সূত্র হিসাবে স্বীকৃত এর রূপ Y= a + bX রয়েছে, যেখানে Y হল নির্ভরশীল চলক (এটি হল ভেরিয়েবল যা Y-অক্ষের উপর যায়), X হল স্বাধীন চলক (অর্থাৎ এটি প্লট করা হয় X-অক্ষ), b হল রেখার ঢাল এবং a হল y-ইন্টারসেপ্ট ( y এর মান যখন x = 0 হবে)।
একটি রেখার ঢাল একটি মান যা স্বাধীন এবং নির্ভরশীল ভেরিয়েবলের মধ্যে পরিবর্তনের হার বর্ণনা করে। ঢাল আমাদের বলে যে কিভাবে নির্ভরশীল পরিবর্তনশীল ( y ) স্বাধীন ( x ) ভেরিয়েবলের প্রতিটি এক-ইউনিট বৃদ্ধির জন্য গড়ে পরিবর্তিত হয়। y -ইন্টারসেপ্টটি নির্ভরশীল ভেরিয়েবলকে বর্ণনা করতে ব্যবহৃত হয় যখন স্বাধীন চলকটি শূন্যের সমান হয়।
b>0 দুটি ভেরিয়েবলের মধ্যে একটি ইতিবাচক সম্পর্ক দেখায়।
আপনি রৈখিক রিগ্রেশনের সমীকরণ পেতে, স্ক্যাটার চার্ট প্লট করতে এবং রিগ্রেশন লাইন আঁকতে এক্সেলের মতো যেকোনো পরিসংখ্যানগত সফ্টওয়্যার ব্যবহার করতে পারেন।
রিগ্রেশন বিশ্লেষণ কিভাবে কাজ করে?
রৈখিক রিগ্রেশন বিন্দুর মধ্য দিয়ে সেরা-ফিটিং সরলরেখা খুঁজে নিয়ে গঠিত। একটি নির্ভরশীল ভেরিয়েবলকে সংজ্ঞায়িত করুন যা আপনি এক বা একাধিক স্বাধীন ভেরিয়েবল দ্বারা প্রভাবিত হচ্ছে বলে অনুমান করেন। এই ভেরিয়েবলের জন্য ডেটাসেট সংগ্রহ করুন।
উদাহরণ 1: চলুন ব্যবহৃত গাড়ী বিক্রয়ের জন্য নিচের তথ্য বিবেচনা করা যাক।
| গাড়ির বয়স (বছরে) | দাম (ডলারে) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
ডেটা দেখে আমরা বলতে পারি যে গাড়ির বয়স বাড়ার সাথে সাথে গাড়ির দাম কমছে।
রিগ্রেশন লাইনের সূত্র হল Y= a + bX, নিচের সূত্রগুলি ব্যবহার করে a এবং b বের করুন
এই সম্পর্কের রৈখিক রিগ্রেশন সমীকরণ হল Y = -557.62125 X + 8356.81293
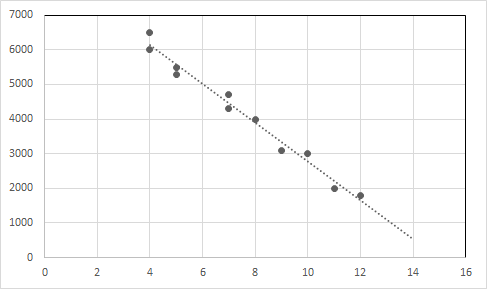
একটি গ্রাফে ডেটা পয়েন্ট এবং রিগ্রেশন লাইন প্লট করুন।
X-অক্ষ: বয়স, Y-অক্ষ: মূল্য
উদাহরণ 2: জন একজন প্লাম্বার। তিনি ভিজিটিং চার্জ হিসাবে $25 ডলার এবং তার ঘন্টায় কাজের চার্জ হিসাবে $35 চার্জ করেন। একটি রৈখিক সমীকরণ যা প্রতিটি ভিজিটের জন্য জন যে পরিমাণ অর্থ উপার্জন করে তা প্রকাশ করে তা হল y = 25 + 35x।
কেন রিগ্রেশন বিশ্লেষণ?