Du wirst es lernen:
Die Regressionsanalyse ist eine Möglichkeit, Variablen zueinander in Beziehung zu setzen. Variablen sind einfach die Informationen, die wir gesammelt haben. Mithilfe der Regressionsanalyse können wir Muster in unseren Daten finden. Es ermöglicht uns, Vorhersagen auf der Grundlage unserer Daten zu treffen. Die statistische Regression ist eine Technik, mit der bestimmt wird, wie eine abhängige Variable von einer oder mehreren unabhängigen Variablen beeinflusst wird. In mathematischer Hinsicht beantwortet die statistische Regression die Frage: Was wird die Auswirkung auf den Wert von Y (der abhängigen Variablen) sein, wenn der Wert von X (der unabhängigen Variablen) geändert wird?
Zum Beispiel wollen wir den Zusammenhang zwischen Alter und Preis von Gebrauchtwagen herausfinden, die letztes Jahr von einem Autohändler verkauft wurden. Wir werden eine negative Beziehung zwischen diesen beiden Variablen sehen. Mit zunehmendem Fahrzeugalter sinken die Preise. In diesem Beispiel sind Autoalter und Autopreis zwei Variablen. Der Autopreis ist vom Alter des Autos abhängig. Was wir finden wollen, ist eine Gleichung, die am besten zu den Daten passt, die wir haben. Ein sehr einfaches Regressionsanalysemodell, das wir für unser Beispiel verwenden können, wird als lineares Modell bezeichnet, das eine einfache lineare Gleichung verwendet, um die Daten anzupassen. Lineare Gleichungen ergeben, wenn sie grafisch dargestellt werden, eine gerade Linie.
Die lineare Regressionsgleichung oder auch Steigungsformel genannt hat die Form Y= a + bX, wobei Y die abhängige Variable ist (das ist die Variable, die auf der Y-Achse verläuft), X die unabhängige Variable (d. h. sie wird auf der Y-Achse aufgetragen). X-Achse), b ist die Steigung der Linie und a ist der y-Achsenabschnitt (der Wert von y , wenn x = 0).
Die Steigung einer Geraden ist ein Wert, der die Änderungsrate zwischen den unabhängigen und abhängigen Variablen beschreibt. Die Steigung sagt uns, wie sich die abhängige Variable ( y ) im Durchschnitt für jede Erhöhung der unabhängigen ( x ) Variablen um eine Einheit ändert. Der y -Achsenabschnitt wird verwendet, um die abhängige Variable zu beschreiben, wenn die unabhängige Variable gleich Null ist.
b>0 zeigt eine positive Beziehung zwischen den beiden Variablen.
Sie können auch jede Statistiksoftware wie Excel verwenden, um die Gleichung für die lineare Regression zu erhalten, das Streudiagramm zu zeichnen und die Regressionslinie zu zeichnen.
Wie funktioniert die Regressionsanalyse?
Die lineare Regression besteht darin, die am besten passende gerade Linie durch die Punkte zu finden. Definieren Sie eine abhängige Variable, von der Sie vermuten, dass sie von einer oder mehreren unabhängigen Variablen beeinflusst wird. Sammeln Sie den Datensatz für diese Variablen.
Beispiel 1: Betrachten wir die folgenden Daten für den Gebrauchtwagenverkauf.
| Fahrzeugalter (in Jahren) | Preis (in Dollar) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Wenn wir uns die Daten ansehen, können wir sagen, dass der Autopreis mit zunehmendem Alter des Autos sinkt.
Die Formel für eine Regressionslinie ist Y= a + bX, leiten Sie a und b mit den folgenden Formeln ab
Die lineare Regressionsgleichung für diese Beziehung ist Y = -557,62125 X + 8356,81293
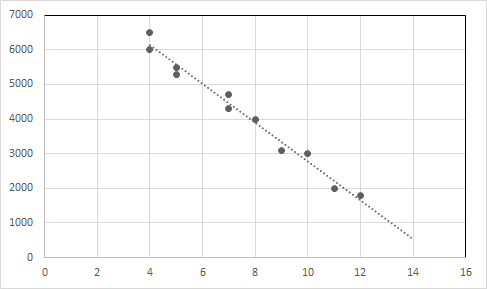
Zeichnen Sie die Datenpunkte und die Regressionslinie in einem Diagramm.
X-Achse: Alter, Y-Achse: Preis
Beispiel 2: John ist Klempner. Er berechnet 25 Dollar als Besuchsgebühr und 35 Dollar als Stundenlohn. Eine lineare Gleichung, die den Gesamtbetrag ausdrückt, den John für jeden Besuch verdient, ist y = 25 + 35x.
Warum die Regressionsanalyse?