Aprenderás:
El análisis de regresión es una forma de relacionar variables entre sí. Las variables son simplemente los bits de información que hemos recopilado. Mediante el uso de análisis de regresión, podemos encontrar patrones en nuestros datos. Nos permite hacer predicciones basadas en nuestros datos. La regresión estadística es una técnica utilizada para determinar cómo una variable dependiente se ve afectada por una o más variables independientes. En términos matemáticos, la regresión estadística responde a la pregunta: ¿Cuál será el impacto en el valor de Y (la variable dependiente) si se cambia el valor de X (la variable independiente)?
Por ejemplo, queremos averiguar la relación entre la antigüedad y el precio de los automóviles usados vendidos el año pasado por un concesionario de automóviles. Veremos una relación negativa entre estas dos variables. A medida que aumenta la edad del automóvil, los precios bajan. En este ejemplo, la antigüedad del automóvil y el precio del automóvil son dos variables. El precio del coche depende de la edad del coche. Lo que queremos encontrar es una ecuación que se ajuste mejor a los datos que tenemos. Un modelo de análisis de regresión muy simple que podemos usar para nuestro ejemplo se llama modelo lineal , que usa una ecuación lineal simple para ajustar los datos. Las ecuaciones lineales cuando se grafican te dan una línea recta.
La ecuación de regresión lineal o también conocida como la fórmula de la pendiente tiene la forma Y= a + bX, donde Y es la variable dependiente (esa es la variable que va en el eje Y), X es la variable independiente (es decir, se grafica en el eje X), b es la pendiente de la línea y a es la intersección en y (el valor de y cuando x = 0).
La pendiente de una línea es un valor que describe la tasa de cambio entre las variables independientes y dependientes. La pendiente nos dice cómo cambia la variable dependiente ( y ) por cada aumento de una unidad en la variable independiente ( x ), en promedio. El intercepto en y se usa para describir la variable dependiente cuando la variable independiente es igual a cero.
b>0 muestra una relación positiva entre las dos variables.
También puede usar cualquier software estadístico como Excel para obtener la ecuación de regresión lineal, trazar el gráfico de dispersión y dibujar la línea de regresión.
¿Cómo funciona el análisis de regresión?
La regresión lineal consiste en encontrar la línea recta que mejor se ajusta a través de los puntos. Defina una variable dependiente que, según su hipótesis, esté influenciada por una o varias variables independientes. Recopile el conjunto de datos para estas variables.
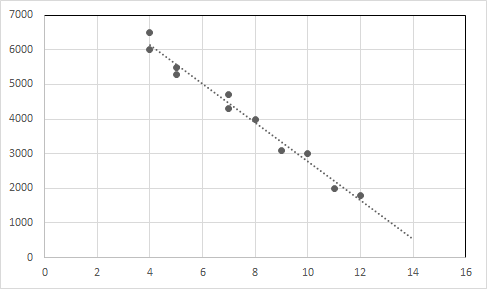
Ejemplo 1: Consideremos los siguientes datos para la venta de autos usados.
| Edad del coche (en años) | Precio (en dólares) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Mirando los datos, podemos decir que el precio del automóvil se reduce con el aumento de la edad del automóvil.
La fórmula para una línea de regresión es Y = a + bX, obtenga a y b usando las fórmulas a continuación
La ecuación de regresión lineal para esta relación es Y = -557.62125 X + 8356.81293
Trace los puntos de datos y la línea de regresión en un gráfico.
Eje X: Edad, Eje Y: Precio
Ejemplo 2: Juan es plomero. Cobra $25 dólares por visita y $35 por horas de trabajo. Una ecuación lineal que expresa la cantidad total de dinero que John gana por cada visita es y = 25 + 35x.
¿Por qué el análisis de regresión?