Tu vas apprendre:
L'analyse de régression est un moyen de relier les variables les unes aux autres. Les variables sont simplement les éléments d'information que nous avons collectés. En utilisant l'analyse de régression, nous pouvons trouver des modèles dans nos données. Cela nous permet de faire des prédictions basées sur nos données. La régression statistique est une technique utilisée pour déterminer comment une variable dépendante est affectée par une ou plusieurs variables indépendantes. En termes mathématiques, la régression statistique répond à la question : quel sera l'impact sur la valeur de Y (la variable dépendante) si la valeur de X (la variable indépendante) est modifiée ?
Par exemple - nous voulons connaître la relation entre l'âge et le prix des voitures d'occasion vendues l'année dernière par un concessionnaire automobile. Nous verrons une relation négative entre ces deux variables. À mesure que l'âge de la voiture augmente, les prix baissent. Dans cet exemple, l'âge de la voiture et le prix de la voiture sont deux variables. Le prix de la voiture dépend de l'âge de la voiture. Ce que nous voulons trouver, c'est une équation qui correspond le mieux aux données dont nous disposons. Un modèle d'analyse de régression très simple que nous pouvons utiliser pour notre exemple est appelé le modèle linéaire , qui utilise une simple équation linéaire pour ajuster les données. Les équations linéaires lorsqu'elles sont représentées graphiquement vous donnent une ligne droite.
L'équation de régression linéaire ou également reconnue comme formule de pente a la forme Y = a + bX, où Y est la variable dépendante (c'est la variable qui va sur l'axe Y), X est la variable indépendante (c'est-à-dire qu'elle est tracée sur le Axe X), b est la pente de la droite et a est l'ordonnée à l'origine (la valeur de y lorsque x = 0).
La pente d'une ligne est une valeur qui décrit le taux de variation entre les variables indépendantes et dépendantes. La pente nous indique comment la variable dépendante ( y ) change pour chaque augmentation d'une unité de la variable indépendante ( x ), en moyenne. L' ordonnée à l'origine est utilisée pour décrire la variable dépendante lorsque la variable indépendante est égale à zéro.
b>0 montre une relation positive entre les deux variables.
Vous pouvez également utiliser n'importe quel logiciel statistique tel qu'Excel pour obtenir l'équation de la régression linéaire, tracer le nuage de points et tracer la ligne de régression.
Comment fonctionne l'analyse de régression ?
La régression linéaire consiste à trouver la droite la mieux ajustée passant par les points. Définissez une variable dépendante dont vous supposez qu'elle est influencée par une ou plusieurs variables indépendantes. Collectez l'ensemble de données pour ces variables.
Exemple 1 : Considérons les données ci-dessous pour la vente de voitures d'occasion.
| Âge de la voiture (en années) | Prix (en dollars) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| dix | 3000 |
| 11 | 2000 |
| 12 | 1800 |
En regardant les données, nous pouvons dire que le prix des voitures diminue avec l'augmentation de l'âge des voitures.
La formule pour une ligne de régression est Y = a + bX, dérivez a et b en utilisant les formules ci-dessous
L'équation de régression linéaire pour cette relation est Y = -557,62125 X + 8356,81293
Tracez les points de données et la ligne de régression dans un graphique.
Axe X : Âge, Axe Y : Prix
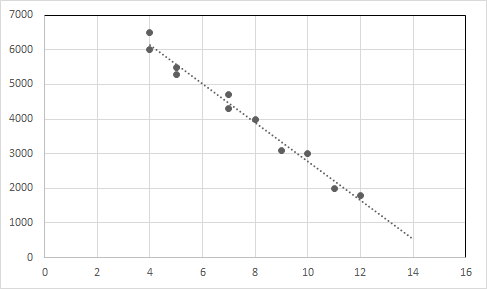
Exemple 2 : Jean est plombier. Il facture 25 $ en frais de visite et 35 $ en frais de travail horaires. Une équation linéaire qui exprime le montant total d'argent que John gagne pour chaque visite est y = 25 + 35x.
Pourquoi l'analyse de régression ?