तुम सीखोगे:
प्रतिगमन विश्लेषण चरों को एक दूसरे से जोड़ने का एक तरीका है। चर हमारे द्वारा एकत्र की गई जानकारी के केवल अंश हैं। प्रतिगमन विश्लेषण का उपयोग करके, हम अपने डेटा में पैटर्न पा सकते हैं। यह हमें अपने डेटा के आधार पर भविष्यवाणियां करने की अनुमति देता है। सांख्यिकीय प्रतिगमन एक तकनीक है जिसका उपयोग यह निर्धारित करने के लिए किया जाता है कि एक आश्रित चर, एक या अधिक स्वतंत्र चर से कैसे प्रभावित होता है। गणितीय शब्दों में सांख्यिकीय प्रतिगमन प्रश्न का उत्तर देता है: यदि X (स्वतंत्र चर) का मान बदल दिया जाता है, तो Y (आश्रित चर) के मान पर क्या प्रभाव पड़ेगा?
उदाहरण के लिए - हम पिछले साल एक कार डीलर द्वारा बेची गई पुरानी कारों की उम्र और कीमत के बीच संबंध का पता लगाना चाहते हैं। हम इन दो चरों के बीच एक नकारात्मक संबंध देखेंगे। जैसे-जैसे कार की उम्र बढ़ती है कीमतें कम होती जाती हैं। इस उदाहरण में, कार की उम्र और कार की कीमत दो चर हैं। कार की कीमत कार की उम्र पर निर्भर करती है। हम जो खोजना चाहते हैं वह एक ऐसा समीकरण है जो हमारे पास मौजूद डेटा के लिए सबसे उपयुक्त है। एक बहुत ही सरल प्रतिगमन विश्लेषण मॉडल जिसे हम अपने उदाहरण के लिए उपयोग कर सकते हैं उसे रैखिक मॉडल कहा जाता है, जो डेटा को फिट करने के लिए एक सरल रैखिक समीकरण का उपयोग करता है। रेखीय समीकरण जब रेखांकन किए जाते हैं तो आपको एक सीधी रेखा मिलती है।
रैखिक प्रतिगमन समीकरण या जिसे ढलान सूत्र के रूप में भी जाना जाता है, का रूप Y = a + bX है, जहां Y आश्रित चर है (यह वह चर है जो Y- अक्ष पर जाता है), X स्वतंत्र चर है (अर्थात इसे पर प्लॉट किया गया है X-अक्ष), b रेखा का ढलान है और a y-अवरोधन है ( y का मान जब x = 0) है।
एक रेखा का ढलान एक मान है जो स्वतंत्र और आश्रित चर के बीच परिवर्तन की दर का वर्णन करता है। ढलान हमें बताता है कि स्वतंत्र ( x ) चर में हर एक-इकाई वृद्धि के लिए आश्रित चर ( y ) कैसे बदलता है, औसतन। y- अवरोधन का उपयोग आश्रित चर का वर्णन करने के लिए किया जाता है जब स्वतंत्र चर शून्य के बराबर होता है।
b>0 दो चरों के बीच एक सकारात्मक संबंध दर्शाता है।
आप रैखिक प्रतिगमन के लिए समीकरण प्राप्त करने, स्कैटर चार्ट को प्लॉट करने और प्रतिगमन रेखा खींचने के लिए एक्सेल जैसे किसी भी सांख्यिकीय सॉफ़्टवेयर का उपयोग कर सकते हैं।
प्रतिगमन विश्लेषण कैसे काम करता है?
रैखिक प्रतिगमन में बिंदुओं के माध्यम से सबसे अच्छी फिटिंग वाली सीधी रेखा को खोजना शामिल है। एक आश्रित चर परिभाषित करें जिसे आप एक या कई स्वतंत्र चर से प्रभावित होने की परिकल्पना करते हैं। इन चरों के लिए डेटासेट एकत्र करें।
उदाहरण 1: पुरानी कारों की बिक्री के लिए नीचे दिए गए आंकड़ों पर विचार करें।
| कार की आयु (वर्षों में) | कीमत (डॉलर में) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 1 1 | 2000 |
| 12 | 1800 |
आंकड़ों को देखते हुए हम कह सकते हैं कि कार की उम्र बढ़ने के साथ कार की कीमत कम हो जाती है।
प्रतिगमन रेखा का सूत्र Y= a + bX है, नीचे दिए गए सूत्रों का उपयोग करके a और b व्युत्पन्न करें
इस संबंध के लिए रैखिक प्रतिगमन समीकरण Y = -557.62125 X + 8356.81293 . है
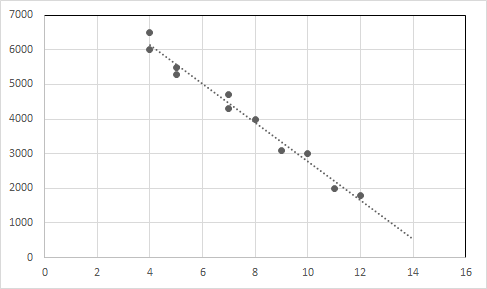
डेटा पॉइंट और रिग्रेशन लाइन को एक ग्राफ में प्लॉट करें।
एक्स-अक्ष: आयु, वाई-अक्ष: मूल्य
उदाहरण 2: जॉन प्लंबर है। वह विज़िटिंग चार्ज के रूप में $25 डॉलर और अपने प्रति घंटा काम करने के शुल्क के रूप में $35 चार्ज करता है। y = 25 + 35x एक रैखिक समीकरण है जो जॉन द्वारा प्रत्येक विज़िट के लिए अर्जित की गई कुल राशि को व्यक्त करता है।
प्रतिगमन विश्लेषण क्यों?