Imparerai:
L'analisi di regressione è un modo per mettere in relazione le variabili tra loro. Le variabili sono semplicemente i bit di informazioni che abbiamo raccolto. Utilizzando l'analisi di regressione, possiamo trovare modelli nei nostri dati. Ci permette di fare previsioni basate sui nostri dati. La regressione statistica è una tecnica utilizzata per determinare in che modo una variabile dipendente è influenzata da una o più variabili indipendenti. In termini matematici, la regressione statistica risponde alla domanda: quale sarà l'impatto sul valore di Y (la variabile dipendente) se il valore di X (la variabile indipendente) viene modificato?
Ad esempio, vogliamo scoprire la relazione tra l'età e il prezzo delle auto usate vendute l'anno scorso da un concessionario di automobili. Vedremo una relazione negativa tra queste due variabili. Con l'aumentare dell'età dell'auto i prezzi scendono. In questo esempio, l'età dell'auto e il prezzo dell'auto sono due variabili. Il prezzo dell'auto dipende dall'età dell'auto. Quello che vogliamo trovare è un'equazione che si adatta meglio ai dati che abbiamo. Un modello di analisi di regressione molto semplice che possiamo utilizzare per il nostro esempio è chiamato modello lineare , che utilizza una semplice equazione lineare per adattare i dati. Le equazioni lineari quando rappresentate graficamente ti danno una linea retta.
L'equazione di regressione lineare o anche riconosciuta come formula della pendenza ha la forma Y= a + bX, dove Y è la variabile dipendente (cioè la variabile che va sull'asse Y), X è la variabile indipendente (cioè è tracciata sull'asse Asse X), b è la pendenza della retta e a è l'intercetta y (il valore di y quando x = 0).
La pendenza di una linea è un valore che descrive il tasso di variazione tra le variabili indipendenti e dipendenti. La pendenza ci dice come cambia in media la variabile dipendente ( y ) per ogni aumento di un'unità nella variabile indipendente ( x ). L' intercetta y viene utilizzata per descrivere la variabile dipendente quando la variabile indipendente è uguale a zero.
b>0 mostra una relazione positiva tra le due variabili.
Puoi anche utilizzare qualsiasi software statistico come Excel per ottenere l'equazione per la regressione lineare, tracciare il grafico a dispersione e tracciare la linea di regressione.
Come funziona l'analisi di regressione?
La regressione lineare consiste nel trovare la retta che meglio si adatta attraverso i punti. Definire una variabile dipendente che si ipotizza sia influenzata da una o più variabili indipendenti. Raccogli il set di dati per queste variabili.
Esempio 1: Consideriamo i dati seguenti per la vendita di auto usate.
| Età dell'auto (in anni) | Prezzo (in dollari) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Guardando i dati possiamo dire che il prezzo dell'auto diminuisce con l'aumentare dell'età dell'auto.
La formula per una retta di regressione è Y= a + bX, deriva a e b utilizzando le formule seguenti
L'equazione di regressione lineare per questa relazione è Y = -557,62125 X + 8356,81293
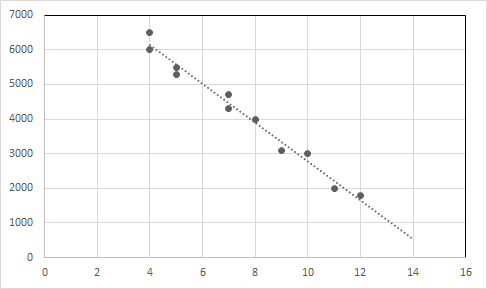
Tracciare i punti dati e la linea di regressione in un grafico.
Asse X: età, asse Y: prezzo
Esempio2: John è un idraulico. Fa pagare $ 25 dollari come spese di visita e $ 35 come spese orarie di lavoro. Un'equazione lineare che esprime la somma totale di denaro che John guadagna per ogni visita è y = 25 + 35x.
Perché l'analisi di regressione?