学習内容:
回帰分析は、変数を相互に関連付ける方法です。変数は、単に収集した情報のビットです。回帰分析を使用すると、データのパターンを見つけることができます。これにより、データに基づいて予測を行うことができます。統計回帰は、従属変数が 1 つ以上の独立変数によってどのように影響を受けるかを判断するために使用される手法です。統計的回帰は数学的に言えば、次の質問に答えます: X (独立変数) の値が変更された場合、Y (従属変数) の値にどのような影響があるでしょうか?
たとえば、自動車ディーラーが昨年販売した中古車の年式と価格の関係を調べたいとします。これら 2 つの変数の間に負の関係があることがわかります。車の年齢が上がるにつれて、価格は下がります。この例では、車の年式と車の価格が 2 つの変数です。車の価格は車の年式によって異なります。私たちが見つけたいのは、私たちが持っているデータに最適な方程式です。この例で使用できる非常に単純な回帰分析モデルは線形モデルと呼ばれ、単純な線形方程式を使用してデータを当てはめます。一次方程式をグラフにすると直線になります。
線形回帰式または勾配式としても認識され、Y= a + bX の形式を持ちます。ここで、Y は従属変数 (Y 軸上にある変数)、X は独立変数 (つまり、 X 軸)、b は直線の傾き、a は y 切片 ( x = 0 の場合のyの値) です。
直線の傾きは、独立変数と従属変数の間の変化率を表す値です。勾配は、平均して、独立変数 ( x ) が 1 単位増加するごとに、従属変数 ( y ) がどのように変化するかを示します。 y切片は、独立変数がゼロに等しい場合の従属変数を表すために使用されます。
b>0 は、2 つの変数間に正の関係があることを示しています。
また、Excel などの統計ソフトウェアを使用して、線形回帰の方程式を取得し、散布図をプロットし、回帰直線を描くこともできます。
回帰分析はどのように機能しますか?
線形回帰は、ポイントを通る最適な直線を見つけることで構成されます。 1 つまたは複数の独立変数によって影響を受けると仮定する従属変数を定義します。これらの変数のデータセットを収集します。
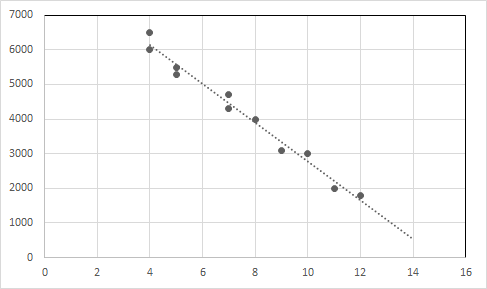
例 1:中古車販売に関する以下のデータを考えてみましょう。
| 車の年齢(年) | 価格(ドル) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000年 |
| 12 | 1800年 |
データを見ると、車の年齢が上がるにつれて車の価格が下がると言えます。
回帰直線の式は Y= a + bX で、以下の式を使用して a と b を導出します。
この関係の線形回帰式は、Y = -557.62125 X + 8356.81293 です。
データ ポイントと回帰直線をグラフにプロットします。
X軸:年齢、Y軸:価格
例 2:ジョンは配管工です。彼は、訪問料金として 25 ドル、時間当たりの作業料金として 35 ドルを請求します。 John が 1 回の訪問で得る合計金額を表す一次方程式は、y = 25 + 35x です。
なぜ回帰分析?