Ти ќе научиш:
Регресивната анализа е начин на поврзување на променливите една со друга. Променливите се едноставно делови од информации што ги собравме. Со користење на регресивна анализа, можеме да најдеме шеми во нашите податоци. Ни овозможува да правиме предвидувања врз основа на нашите податоци. Статистичка регресија е техника која се користи за да се одреди како на зависна променлива влијае една или повеќе независни променливи. Во математичка смисла, Статистичката регресија одговара на прашањето: Какво ќе биде влијанието врз вредноста на Y (зависната променлива) ако вредноста на X (независната променлива) се промени?
На пример - сакаме да ја дознаеме врската помеѓу староста и цената на половните автомобили продадени минатата година од дилер на автомобили. Ќе видиме негативна врска помеѓу овие две променливи. Како што се зголемува староста на автомобилите, цените се намалуваат. Во овој пример, староста на автомобилот и цената на автомобилот се две варијабли. Цената на автомобилот зависи од староста на автомобилот. Она што сакаме да го најдеме е равенка која најдобро одговара на податоците што ги имаме. Многу едноставен модел за регресивна анализа што можеме да го користиме за нашиот пример се нарекува линеарен модел , кој користи едноставна линеарна равенка за да ги собере податоците. Линеарните равенки кога се графички ви даваат права линија.
Линеарна регресивна равенка или исто така препознаена како формула за наклон има форма Y= a + bX, каде што Y е зависната променлива (тоа е променливата што оди на Y-оската), X е независна променлива (т.е. е нацртана на X-оска), b е наклонот на правата и a е y-пресекот (вредноста на y кога x = 0).
Наклонот на линијата е вредност што ја опишува стапката на промена помеѓу независните и зависните променливи. Наклонот ни кажува како зависната променлива ( y ) се менува за секое зголемување од една единица во независната ( x ) променлива, во просек. Пресекот y се користи за опишување на зависната променлива кога независната променлива е еднаква на нула.
b>0 покажува позитивна врска помеѓу двете променливи.
Можете исто така да користите било кој статистички софтвер како excel за да ја добиете равенката за линеарна регресија, да ја нацртате табелата за расејување и да ја нацртате регресивната линија.
Како функционира регресивната анализа?
Линеарната регресија се состои од наоѓање на права линија која најдобро одговара низ точките. Дефинирајте зависна променлива за која претпоставувате дека е под влијание на една или неколку независни променливи. Соберете ја базата на податоци за овие променливи.
Пример 1: Да ги разгледаме долунаведените податоци за продажбата на половни автомобили.
| Старост на автомобилот (во години) | Цена (во долари) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 година |
| 12 | 1800 година |
Гледајќи ги податоците можеме да кажеме дека цената на автомобилот се намалува со зголемувањето на староста на автомобилите.
Формулата за регресивна линија е Y= a + bX, изведете a и b користејќи ги формулите подолу
Линеарната регресивна равенка за оваа врска е Y = -557,62125 X + 8356,81293
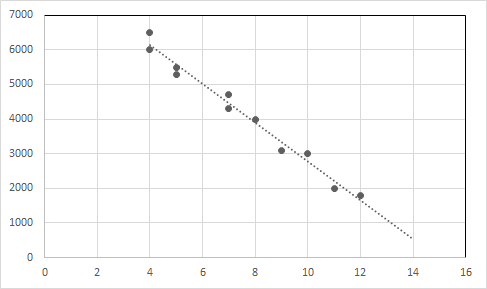
Подгответе ги точките на податоци и линијата за регресија во графикон.
X-оска : возраст, Y-оска: Цена
Пример2: Џон е водоводџија. Тој наплаќа 25 долари за посета и 35 долари како работен час. Линеарна равенка што го изразува вкупниот износ на пари што Џон го заработува за секоја посета е y = 25 + 35x.
Зошто регресивна анализа?