Та сурах болно:
Регрессийн шинжилгээ нь хувьсагчдыг хооронд нь холбох арга юм. Хувьсагч нь бидний цуглуулсан мэдээллийн хэсэг юм. Регрессийн шинжилгээг ашигласнаар бид өгөгдлөөсөө хэв маягийг олж чадна. Энэ нь бидний өгөгдөл дээр үндэслэн таамаглал гаргах боломжийг бидэнд олгодог. Статистикийн регресс нь нэг буюу хэд хэдэн бие даасан хувьсагчаас хамааралтай хувьсагчд хэрхэн нөлөөлж байгааг тодорхойлоход ашигладаг арга юм. Математикийн хэллэгээр статистикийн регресс нь дараах асуултад хариулдаг: Хэрэв X (бие даасан хувьсагч)-ийн утга өөрчлөгдсөн бол Y (хамааралтай хувьсагч)-ийн утгад ямар нөлөө үзүүлэх вэ?
Жишээлбэл, бид өнгөрсөн жил автомашины борлуулагчийн борлуулсан хуучин автомашины нас, үнэ хоорондын хамаарлыг олж мэдэхийг хүсч байна. Бид эдгээр хоёр хувьсагчийн хооронд сөрөг хамаарлыг харах болно. Машины нас ахих тусам үнэ буурдаг. Энэ жишээнд машины нас, үнэ хоёр хувьсагч байна. Машины үнэ нь машины наснаас хамаарна. Бидний олохыг хүсч байгаа зүйл бол бидэнд байгаа өгөгдөлд хамгийн сайн тохирох тэгшитгэл юм. Бидний жишээнд ашиглаж болох маш энгийн регрессийн шинжилгээний загварыг шугаман загвар гэж нэрлэдэг бөгөөд энэ нь өгөгдөлд тохирох энгийн шугаман тэгшитгэлийг ашигладаг. Шугаман тэгшитгэлийг графикаар зурах нь шулуун шугамыг өгдөг.
Шугаман регрессийн тэгшитгэл эсвэл налуугийн томьёо нь Y= a + bX хэлбэртэй байх ба энд Y нь хамааралтай хувьсагч (энэ нь Y тэнхлэгт хамаарах хувьсагч), X нь бие даасан хувьсагч (өөрөөр хэлбэл энэ нь тэнхлэг дээр зурсан) юм. X тэнхлэг), b нь шулууны налуу, a нь y-н огтлолцол ( x = 0 үед y -ийн утга).
Шугамын налуу нь бие даасан болон хамааралтай хувьсагчдын хоорондох өөрчлөлтийн хурдыг тодорхойлдог утга юм. Налуу нь бие даасан ( x ) хувьсагчийн нэг нэгжийн өсөлт бүрт хамааралтай хувьсагч ( y ) хэрхэн өөрчлөгдөхийг бидэнд хэлдэг. Бие даасан хувьсагч нь тэгтэй тэнцүү байх үед хамааралтай хувьсагчийг тодорхойлоход y - intercept ашигладаг.
b>0 нь хоёр хувьсагчийн хооронд эерэг хамаарлыг харуулж байна.
Та мөн шугаман регрессийн тэгшитгэлийг авах, тархалтын диаграммыг зурах, регрессийн шугамыг зурахын тулд excel гэх мэт статистикийн дурын программыг ашиглаж болно.
Регрессийн шинжилгээ хэрхэн ажилладаг вэ?
Шугаман регресс нь цэгүүдийн дундуур хамгийн сайн тохирох шулуун шугамыг олохоос бүрдэнэ. Нэг буюу хэд хэдэн бие даасан хувьсагчийн нөлөөлөлд өртсөн гэж таамаглаж буй хамааралтай хувьсагчийг тодорхойл. Эдгээр хувьсагчийн мэдээллийн багцыг цуглуул.
Жишээ 1: Хуучин автомашины борлуулалтын талаарх доорх мэдээллийг авч үзье.
| Машины нас (жилээр) | Үнэ (доллараар) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Мэдээллийг харахад машины нас ахих тусам машины үнэ буурдаг гэж хэлж болно.
Регрессийн шугамын томъёо нь Y= a + bX бөгөөд доорх томьёог ашиглан a ба b-г гарга
Энэ хамаарлын шугаман регрессийн тэгшитгэл нь Y = -557.62125 X + 8356.81293 байна.
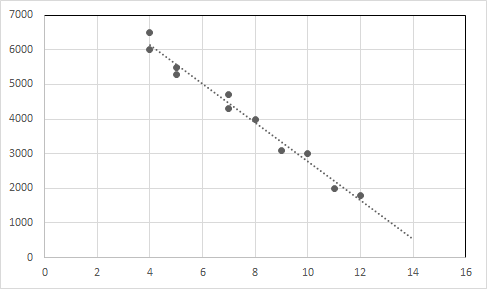
Өгөгдлийн цэгүүд болон регрессийн шугамыг графикаар зур.
X тэнхлэг : Нас, Y тэнхлэг : Үнэ
Жишээ 2: Жон бол сантехникч. Тэрээр зочлоход 25 доллар, цагийн ажилдаа 35 доллар авдаг. Жонны айлчлал болгонд олох нийт мөнгөний хэмжээг илэрхийлсэн шугаман тэгшитгэл нь y = 25 + 35x юм.
Яагаад регрессийн шинжилгээ хийдэг вэ?