Back to the topics list

စာရင်းအင်းဆုတ်ယုတ်

သင်ယူရလိမ့်မည်-

• စာရင်းအင်းဆိုင်ရာ ဆုတ်ယုတ်မှုဆိုသည်မှာ အဘယ်နည်း။
• linear regression equation နှင့် ၎င်း၏ ဆင်းသက်လာခြင်း
• ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာမှုကို အသုံးပြုခြင်း။

ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာခြင်း သည် တစ်ခုနှင့်တစ်ခု ကိန်းရှင်များကို ဆက်စပ်ပေးသည့် နည်းလမ်းတစ်ခုဖြစ်သည်။ ကိန်းရှင်များသည် ကျွန်ုပ်တို့စုဆောင်းထားသော အချက်အလက်အနည်းငယ်မျှသာဖြစ်သည်။ ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာမှုကို အသုံးပြုခြင်းဖြင့် ကျွန်ုပ်တို့၏ဒေတာတွင် ပုံစံများကို ရှာဖွေနိုင်သည်။ ကျွန်ုပ်တို့၏ဒေတာကိုအခြေခံ၍ ခန့်မှန်းချက်များကို ပြုလုပ်နိုင်စေပါသည်။ Statistical Regression သည် အမှီအခိုကင်းသော ကိန်းရှင်တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော အမှီအခိုကင်းသော ကိန်းရှင်များမှ မည်ကဲ့သို့ အကျိုးသက်ရောက်သည်ကို ဆုံးဖြတ်ရန် အသုံးပြုသည့် နည်းလမ်းတစ်ခုဖြစ်သည်။ သင်္ချာအသုံးအနှုန်းများတွင် Statistical Regression သည် မေးခွန်းကိုဖြေဆိုသည်- X ၏တန်ဖိုး (လွတ်လပ်သောကိန်းရှင်) ကိုပြောင်းလဲပါက Y တန်ဖိုးအပေါ် မည်သို့အကျိုးသက်ရောက်မှုရှိမည်နည်း။

ဥပမာ- ကားရောင်းသူမှ ယမန်နှစ်က ရောင်းချခဲ့သော ကားဟောင်းများ၏ အသက်နှင့် စျေးနှုန်းအကြား ဆက်စပ်မှုကို ကျွန်ုပ်တို့ ရှာဖွေလိုပါသည်။ ဤကိန်းရှင်နှစ်ခုကြားတွင် အနုတ်လက္ခဏာဆောင်သော ဆက်နွယ်မှုကို ကျွန်ုပ်တို့တွေ့ရပါမည်။ ကားသက်တမ်းတိုးလာတာနဲ့အမျှ ကားဈေးတွေကျလာတယ်။ ဤဥပမာတွင် ကားအသက်နှင့် ကားစျေးနှုန်းသည် ပြောင်းလဲနိုင်သော နှစ်မျိုးဖြစ်သည်။ ကားစျေးနှုန်းသည် ကားအသက်အရွယ်ပေါ်မူတည်ပါသည်။ ကျွန်ုပ်တို့ရှာဖွေလိုသည်မှာ ကျွန်ုပ်တို့ရှိဒေတာနှင့် အသင့်တော်ဆုံး ညီမျှခြင်းတစ်ခုဖြစ်သည်။ ကျွန်ုပ်တို့၏နမူနာအတွက် အသုံးပြုနိုင်သည့် အလွန်ရိုးရှင်းသော ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာမှုပုံစံကို လိုင်းနားမော်ဒယ် ဟုခေါ်သည်၊ ဒေတာနှင့်ကိုက်ညီရန် ရိုးရှင်းသောမျဉ်းကြောင်းညီမျှခြင်းကိုအသုံးပြုသည်။ ဂရပ်ဖစ်ပြသောအခါ မျဉ်းဖြောင့်ညီမျှခြင်းများသည် သင့်အား မျဉ်းဖြောင့်တစ်ခုပေးသည်။

linear regression equation သို့မဟုတ် slope formula တွင် Y=a + bX ပုံစံပါရှိသည်၊ Y သည် မှီခိုကိန်းရှင် (၎င်းသည် Y-ဝင်ရိုးပေါ်ရှိ ကိန်းရှင်ဖြစ်သည်)၊ X သည် အမှီအခိုကင်းသော ကိန်းရှင်ဖြစ်သည် (ဆိုလိုသည်မှာ ၎င်းကို အပေါ်တွင် ပုံဖော်ထားသည်။ X-axis) b သည် မျဉ်း၏ လျှောစောက်ဖြစ်ပြီး a သည် y-ကြားဖြတ် ( x = 0 ဖြစ်သောအခါ y ၏တန်ဖိုး)။

မျဉ်းတစ်ကြောင်း၏ လျှောစောက် သည် အမှီအခိုကင်းသော နှင့် အမှီပြုသော ကိန်းရှင်များအကြား ပြောင်းလဲမှုနှုန်းကို ဖော်ပြသည့် တန်ဖိုးတစ်ခုဖြစ်သည်။ slope သည် ပျမ်းမျှအားဖြင့် လွတ်လပ်သော ( x ) variable တွင် တစ်ယူနစ်တိုးတိုင်းအတွက် မှီခို variable ( y ) ပြောင်းလဲပုံကို ပြောပြသည်။ အမှီအခိုကင်းသောကိန်းရှင်သည် သုညနှင့်ညီမျှသောအခါ y -intercept ကို မှီခိုကိန်းရှင်ကိုဖော်ပြရန်အသုံးပြုသည်။

\(a = \frac{(\Sigma y)(\Sigma x^2) - (\Sigma x) (\Sigma xy)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

\(b = \frac{n(\Sigma xy) - (\Sigma x) (\Sigma y)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

b>0 သည် ကိန်းရှင်နှစ်ခုကြားတွင် အပြုသဘောဆောင်သော ဆက်ဆံရေးကို ပြသသည်။

linear regression အတွက် equation ကိုရရန်၊ scatter chart ကိုဆွဲရန်နှင့် regression line ကိုဆွဲရန် excel ကဲ့သို့သော ကိန်းဂဏန်းဆိုင်ရာဆော့ဖ်ဝဲလ်ကို အသုံးပြုနိုင်သည်။

ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာမှု ဘယ်လိုအလုပ်လုပ်သလဲ။
Linear regression သည် အမှတ်များမှတဆင့် အသင့်တော်ဆုံး မျဉ်းဖြောင့်ကို ရှာဖွေခြင်း ပါဝင်သည်။ အမှီအခိုကင်းသော ကိန်းရှင်တစ်ခု သို့မဟုတ် အများအပြားက လွှမ်းမိုးနေသည်ဟု သင်ယူဆသည့် မှီခိုကိန်းရှင်ကို သတ်မှတ်ပါ။ ဤကိန်းရှင်များအတွက် ဒေတာအတွဲကို စုဆောင်းပါ။
ဥပမာ 1- ကားဟောင်းရောင်းခြင်းအတွက် အောက်ဖော်ပြပါ အချက်အလက်ကို သုံးသပ်ကြည့်ရအောင်။

ဒေတာကိုကြည့်လျှင် ကားစျေးသည် ကားသက်တမ်းတိုးလာသည်နှင့်အမျှ စျေးလျော့သွားသည်ဟု ဆိုနိုင်သည်။

ဆုတ်ယုတ်မှုမျဉ်းအတွက် ဖော်မြူလာမှာ Y= a + bX ဖြစ်ပြီး၊ အောက်ဖော်ပြပါ ဖော်မြူလာများကို အသုံးပြု၍ a နှင့် b ကို ရယူသည်

\(a = \frac{(\Sigma y)(\Sigma x^2) - (\Sigma x) (\Sigma xy)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

\(b = \frac{n(\Sigma xy) - (\Sigma x) (\Sigma y)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

ဤဆက်နွယ်မှုအတွက် မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ Y = -557.62125 X + 8356.81293

ဒေတာအချက်များနှင့် ဆုတ်ယုတ်မှုမျဉ်းကို ဂရပ်တစ်ခုတွင် ရေးဆွဲပါ။

X-axis : အသက်၊ Y-axis : ဈေးနှုန်း

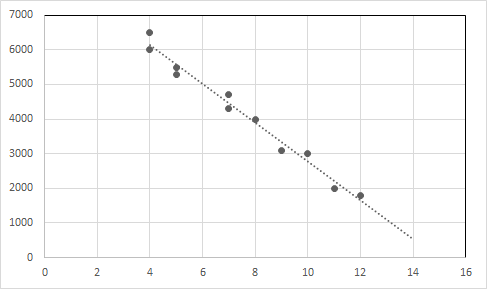
ဥပမာ ၂- ယောဟန်သည် ရေပိုက်သမားဖြစ်သည်။ အလည်အပတ်စရိတ်အဖြစ် ၂၅ ဒေါ်လာနှင့် ၎င်း၏ တစ်နာရီ အလုပ်ခအဖြစ် ၃၅ ဒေါ်လာ ကောက်ခံသည်။ လည်ပတ်မှုတစ်ခုစီအတွက် John ရရှိသော စုစုပေါင်းငွေပမာဏကို ဖော်ပြသည့်မျဉ်းကြောင်းညီမျှခြင်းမှာ y = 25 + 35x ဖြစ်သည်။

အဘယ်ကြောင့် ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာခြင်း ၊

• အမှီအခိုကင်းသော ကိန်းရှင်(များ) သည် မှီခိုကိန်းရှင်တစ်ခုပေါ်တွင် ရှိသော အကျိုးသက်ရောက်မှုကို ဖော်ထုတ်ရန် ဆုတ်ယုတ်မှုကို အသုံးပြုနိုင်သည်။ ဥပမာ- ဆေးပမာဏနှင့် အကျိုးသက်ရောက်မှု၊ အရောင်းနှင့် စျေးကွက်ရှာဖွေရေးအသုံးစရိတ် သို့မဟုတ် အသက်နှင့် ဝင်ငွေအကြား ဆက်နွယ်မှု၏ ခိုင်ခံ့မှုကား အဘယ်နည်း။
• အပြောင်းအလဲများ၏ သက်ရောက်မှု သို့မဟုတ် သက်ရောက်မှုကို ခန့်မှန်းရန် ၎င်းကို အသုံးပြုနိုင်သည်။ ဆိုလိုသည်မှာ၊ ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှုသည် တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော အမှီအခိုကင်းသော ကိန်းရှင်တစ်ခုတွင် ပြောင်းလဲမှုတစ်ခုနှင့်အတူ မှီခိုပြောင်းလဲနိုင်သော ပြောင်းလဲမှုများ မည်မျှရှိသည်ကို နားလည်ရန် ကူညီပေးသည်။ ဥပမာ - စျေးကွက်ရှာဖွေရေးတွင် အသုံးပြုသည့် နောက်ထပ် $1000 တစ်ခုစီအတွက် အပိုအရောင်းဝင်ငွေ မည်မျှရနိုင်မည်နည်း။
• ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာမှုသည် ခေတ်ရေစီးကြောင်းများနှင့် အနာဂတ်တန်ဖိုးများကို ခန့်မှန်းပေးသည်။ ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာချက်သည် အမှတ်ခန့်မှန်းချက်များကို ရယူရန် အသုံးပြုနိုင်သည်။ ဥပမာအားဖြင့်၊ ၆ လအတွင်း ရွှေဈေးက ဘယ်လိုရှိမလဲ။