तपाईंले सिक्नुहुनेछ:
प्रतिगमन विश्लेषण एक अर्कासँग चरहरू सम्बन्धित गर्ने तरिका हो। चरहरू केवल हामीले सङ्कलन गरेका जानकारीका बिटहरू हुन्। प्रतिगमन विश्लेषण प्रयोग गरेर, हामी हाम्रो डेटामा ढाँचाहरू फेला पार्न सक्छौं। यसले हामीलाई हाम्रो डाटामा आधारित भविष्यवाणी गर्न अनुमति दिन्छ। सांख्यिकीय प्रतिगमन एक आश्रित चर कसरी एक वा बढी स्वतन्त्र चर द्वारा प्रभावित छ भनेर निर्धारण गर्न प्रयोग गरिने प्रविधि हो। गणितीय सर्तहरूमा सांख्यिकीय प्रतिगमनले प्रश्नको जवाफ दिन्छ: यदि X (स्वतन्त्र चर) को मान परिवर्तन भयो भने Y (निर्भर चल) को मूल्यमा कस्तो प्रभाव पर्छ?
उदाहरण को लागी - हामी एक कार डीलर द्वारा गत वर्ष बेचेको प्रयोग कारहरु को उमेर र मूल्य बीचको सम्बन्ध पत्ता लगाउन चाहन्छौं। हामी यी दुई चरहरू बीचको नकारात्मक सम्बन्ध देख्नेछौं। कारको उमेर बढ्दै जाँदा मूल्य घट्दै जान्छ। यस उदाहरणमा, कारको उमेर र कार मूल्य दुई चर हुन्। कार मूल्य कार उमेर मा निर्भर गर्दछ। हामी के खोज्न चाहन्छौं त्यो एक समीकरण हो जुन हामीसँग भएको डेटामा राम्रोसँग फिट हुन्छ। एक धेरै सरल रिग्रेसन विश्लेषण मोडेल जुन हामीले हाम्रो उदाहरणको लागि प्रयोग गर्न सक्छौं रैखिक मोडेल भनिन्छ, जसले डेटा फिट गर्न सरल रैखिक समीकरण प्रयोग गर्दछ। रेखाचित्र समीकरणले तपाईंलाई सीधा रेखा दिन्छ।
रैखिक प्रतिगमन समीकरण वा ढलान सूत्रको रूपमा पनि पहिचान गरिएकोमा Y= a + bX फारम छ, जहाँ Y निर्भर चल हो (त्यो चर हो जुन Y-अक्षमा जान्छ), X स्वतन्त्र चर हो (अर्थात यो मा प्लट गरिएको छ। X-axis), b रेखाको ढलान हो र a y-अवरोधन हो ( x = 0 हुँदा y को मान)।
रेखाको ढलान एक मान हो जसले स्वतन्त्र र निर्भर चरहरू बीचको परिवर्तनको दरलाई वर्णन गर्दछ। ढलानले हामीलाई बताउँछ कसरी निर्भर चल ( y ) स्वतन्त्र ( x ) चरमा प्रत्येक एक-इकाइ वृद्धिको लागि औसतमा परिवर्तन हुन्छ। स्वतन्त्र चर शून्य बराबर हुँदा निर्भर चर वर्णन गर्न y -intercept प्रयोग गरिन्छ।
b>0 ले दुई चरहरू बीचको सकारात्मक सम्बन्ध देखाउँछ।
तपाईले कुनै पनि सांख्यिकीय सफ्टवेयर प्रयोग गर्न सक्नुहुन्छ जस्तै एक्सेल रैखिक प्रतिगमनको लागि समीकरण प्राप्त गर्न, स्क्याटर चार्ट प्लट गर्न, र प्रतिगमन रेखा कोर्न।
रिग्रेसन विश्लेषणले कसरी काम गर्छ?
रैखिक प्रतिगमन बिन्दुहरू मार्फत उत्तम-फिटिंग सीधा रेखा फेला पार्न समावेश गर्दछ। एक निर्भर चर परिभाषित गर्नुहोस् जुन तपाइँ एक वा धेरै स्वतन्त्र चर द्वारा प्रभावित भएको परिकल्पना गर्नुहुन्छ। यी चरहरूको लागि डाटासेट सङ्कलन गर्नुहोस्।
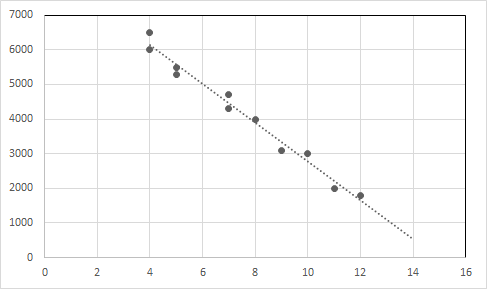
उदाहरण १: प्रयोग गरिएको कार बिक्रीको लागि तलको डेटालाई विचार गरौं।
| कारको उमेर (वर्षमा) | मूल्य (डलरमा) |
| ४ | ६५०० |
| ४ | ६००० |
| ५ | ५५०० |
| ५ | ५३०० |
| ७ | ४७०० |
| ७ | ४३०० |
| ८ | ४००० |
| ९ | ३१०० |
| १० | 3000 |
| ११ | २००० |
| १२ | १८०० |
तथ्याङ्क हेर्दा हामी भन्न सक्छौं कि कारको उमेर बढ्दै जाँदा कारको मूल्य घट्छ।
प्रतिगमन रेखाको लागि सूत्र Y= a + bX हो, तलको सूत्रहरू प्रयोग गरेर a र b निकाल्नुहोस्
यो सम्बन्धको लागि रैखिक प्रतिगमन समीकरण Y = -557.62125 X + 8356.81293 हो।
ग्राफमा डेटा बिन्दुहरू र प्रतिगमन रेखा प्लट गर्नुहोस्।
X-अक्ष: उमेर, Y-अक्ष: मूल्य
उदाहरण २: जोन एक प्लम्बर हो। उसले $25 डलर भिजिटिङ चार्ज र $35 आफ्नो घण्टाको कामको शुल्कको रूपमा लिन्छ। जोनले प्रत्येक भ्रमणको लागि कमाउने कुल रकमलाई व्यक्त गर्ने रैखिक समीकरण y = 25 + 35x हो।
किन प्रतिगमन विश्लेषण?