Je leert:
Regressieanalyse is een manier om variabelen aan elkaar te relateren. Variabelen zijn gewoon de stukjes informatie die we hebben verzameld. Door gebruik te maken van regressieanalyse kunnen we patronen in onze data vinden. Het stelt ons in staat om voorspellingen te doen op basis van onze gegevens. Statistische regressie is een techniek die wordt gebruikt om te bepalen hoe een afhankelijke variabele wordt beïnvloed door een of meer onafhankelijke variabelen. In wiskundige termen beantwoordt statistische regressie de vraag: wat is de impact op de waarde van Y (de afhankelijke variabele) als de waarde van X (de onafhankelijke variabele) wordt gewijzigd?
We willen bijvoorbeeld weten wat de relatie is tussen de leeftijd en de prijs van gebruikte auto's die vorig jaar door een autodealer zijn verkocht. We zullen een negatief verband zien tussen deze twee variabelen. Naarmate de auto ouder wordt, dalen de prijzen. In dit voorbeeld zijn autoleeftijd en autoprijs twee variabelen. De autoprijs is afhankelijk van de leeftijd van de auto. Wat we willen vinden is een vergelijking die het beste past bij de gegevens die we hebben. Een heel eenvoudig regressieanalysemodel dat we voor ons voorbeeld kunnen gebruiken, wordt het lineaire model genoemd, dat een eenvoudige lineaire vergelijking gebruikt om de gegevens te passen. Lineaire vergelijkingen geven je een rechte lijn als je ze in een grafiek zet.
Lineaire regressievergelijking of ook herkend als de hellingsformule heeft de vorm Y= a + bX, waarbij Y de afhankelijke variabele is (dat is de variabele die op de Y-as staat), X de onafhankelijke variabele is (dwz het is uitgezet op de X-as), b is de helling van de lijn en a is het y-snijpunt (de waarde van y wanneer x = 0).
De helling van een lijn is een waarde die de veranderingssnelheid tussen de onafhankelijke en afhankelijke variabelen beschrijft. De helling vertelt ons hoe de afhankelijke variabele ( y ) gemiddeld verandert voor elke toename van één eenheid in de onafhankelijke ( x ) variabele. Het y -snijpunt wordt gebruikt om de afhankelijke variabele te beschrijven wanneer de onafhankelijke variabele gelijk is aan nul.
b>0 toont een positief verband tussen de twee variabelen.
U kunt ook statistische software zoals Excel gebruiken om de vergelijking voor lineaire regressie te krijgen, het spreidingsdiagram te plotten en de regressielijn te tekenen.
Hoe werkt regressieanalyse?
Lineaire regressie bestaat uit het vinden van de best passende rechte lijn door de punten. Definieer een afhankelijke variabele waarvan u vermoedt dat deze wordt beïnvloed door een of meer onafhankelijke variabelen. Verzamel de dataset voor deze variabelen.
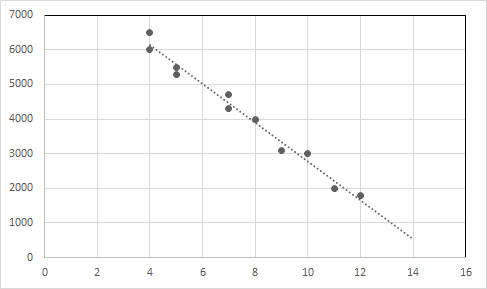
Voorbeeld 1: Laten we eens kijken naar de onderstaande gegevens voor de verkoop van gebruikte auto's.
| Leeftijd auto (in jaren) | Prijs (in dollars) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Als we naar de gegevens kijken, kunnen we zeggen dat de autoprijs daalt met de toename van de leeftijd van de auto.
De formule voor een regressielijn is Y= a + bX, leid a en b af met behulp van onderstaande formules
De lineaire regressievergelijking voor deze relatie is Y = -557.62125 X + 8356.81293
Zet de gegevenspunten en de regressielijn in een grafiek.
X-as: Leeftijd, Y-as: Prijs
Voorbeeld 2: John is een loodgieter. Hij rekent $ 25 dollar als bezoekkosten en $ 35 als zijn uurloon. Een lineaire vergelijking die de totale hoeveelheid geld uitdrukt die John voor elk bezoek verdient, is y = 25 + 35x.
Waarom de regressieanalyse?