Nauczysz się:
Analiza regresji to sposób na powiązanie zmiennych ze sobą. Zmienne to po prostu bity informacji, które zebraliśmy. Korzystając z analizy regresji, możemy znaleźć wzorce w naszych danych. Pozwala nam przewidywać na podstawie naszych danych. Regresja statystyczna to technika używana do określenia, w jaki sposób na zmienną zależną wpływa jedna lub więcej zmiennych niezależnych. W kategoriach matematycznych regresja statystyczna odpowiada na pytanie: Jaki będzie wpływ na wartość Y (zmiennej zależnej), jeśli zmieni się wartość X (zmiennej niezależnej)?
Na przykład - chcemy dowiedzieć się, jaka jest zależność między wiekiem a ceną używanych samochodów sprzedanych w zeszłym roku przez dealera samochodowego. Zobaczymy ujemną zależność między tymi dwiema zmiennymi. Wraz ze wzrostem wieku samochodu ceny spadają. W tym przykładzie wiek samochodu i cena samochodu to dwie zmienne. Cena samochodu uzależniona jest od wieku auta. Chcemy znaleźć równanie, które najlepiej pasuje do danych, które mamy. Bardzo prosty model analizy regresji, którego możemy użyć w naszym przykładzie, nazywa się modelem liniowym , który wykorzystuje proste równanie liniowe w celu dopasowania danych. Równania liniowe po przedstawieniu na wykresie dają linię prostą.
Równanie regresji liniowej lub też uznawane za wzór nachylenia ma postać Y= a + bX, gdzie Y jest zmienną zależną (czyli zmienną, która biegnie po osi Y), X jest zmienną niezależną (tzn. oś X), b to nachylenie linii, a a to punkt przecięcia z osią y (wartość y , gdy x = 0).
Nachylenie linii to wartość opisująca tempo zmian między zmiennymi niezależnymi i zależnymi. Nachylenie mówi nam, jak średnio zmienia się zmienna zależna ( y ) dla każdego wzrostu zmiennej niezależnej ( x ) o jedną jednostkę. Punkt przecięcia z osią y jest używany do opisania zmiennej zależnej, gdy zmienna niezależna jest równa zeru.
b>0 pokazuje pozytywny związek między dwiema zmiennymi.
Możesz także użyć dowolnego oprogramowania statystycznego, takiego jak Excel, aby uzyskać równanie regresji liniowej, wykreślić wykres punktowy i narysować linię regresji.
Jak działa analiza regresji?
Regresja liniowa polega na znalezieniu najlepiej dopasowanej linii prostej przechodzącej przez punkty. Zdefiniuj zmienną zależną, na którą, jak przypuszczasz, ma wpływ jedna lub kilka zmiennych niezależnych. Zbierz zestaw danych dla tych zmiennych.
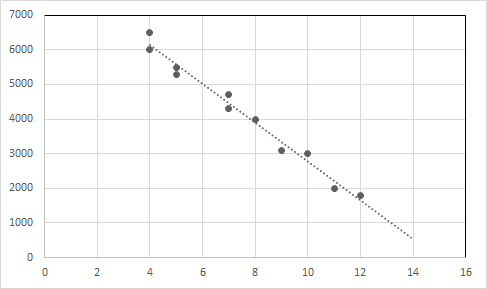
Przykład 1: Rozważmy poniższe dane dotyczące sprzedaży używanego samochodu.
| Wiek samochodu (w latach) | Cena (w dolarach) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Patrząc na dane można stwierdzić, że cena samochodu spada wraz z wiekiem samochodu.
Wzór na linię regresji to Y= a + bX, wyprowadź aib korzystając z poniższych wzorów
Równanie regresji liniowej dla tej zależności to Y = -557,62125 X + 8356,81293
Narysuj punkty danych i linię regresji na wykresie.
Oś X: wiek, oś Y: cena
Przykład 2: Jan jest hydraulikiem. Pobiera 25 dolarów jako opłatę za wizytę i 35 dolarów jako godzinową opłatę roboczą. Równanie liniowe, które wyraża całkowitą kwotę pieniędzy, jaką Jan zarabia za każdą wizytę, to y = 25 + 35x.
Dlaczego analiza regresji?