Você vai aprender:
A análise de regressão é uma forma de relacionar variáveis entre si. Variáveis são simplesmente os bits de informação que coletamos. Ao usar a análise de regressão, podemos encontrar padrões em nossos dados. Ele nos permite fazer previsões com base em nossos dados. A regressão estatística é uma técnica usada para determinar como uma variável dependente é afetada por uma ou mais variáveis independentes. Em termos matemáticos, a Regressão Estatística responde à pergunta: Qual será o impacto no valor de Y (a variável dependente) se o valor de X (a variável independente) for alterado?
Por exemplo - queremos descobrir a relação entre a idade e o preço dos carros usados vendidos no ano passado por um revendedor de carros. Veremos uma relação negativa entre essas duas variáveis. À medida que a idade do carro aumenta, os preços caem. Neste exemplo, a idade do carro e o preço do carro são duas variáveis. O preço do carro depende da idade do carro. O que queremos encontrar é uma equação que melhor se ajuste aos dados que temos. Um modelo de análise de regressão muito simples que podemos usar para nosso exemplo é chamado de modelo linear , que usa uma equação linear simples para ajustar os dados. Equações lineares quando representadas graficamente fornecem uma linha reta.
A equação de regressão linear ou também reconhecida como a fórmula do declive tem a forma Y= a + bX, onde Y é a variável dependente (que é a variável que vai no eixo Y), X é a variável independente (ou seja, é plotada no eixo X), b é a inclinação da linha e a é a interseção em y (o valor de y quando x = 0).
A inclinação de uma linha é um valor que descreve a taxa de variação entre as variáveis independentes e dependentes. A inclinação nos diz como a variável dependente ( y ) muda para cada aumento de uma unidade na variável independente ( x ), em média. A interceptação y é usada para descrever a variável dependente quando a variável independente é igual a zero.
b>0 mostra uma relação positiva entre as duas variáveis.
Você também pode usar qualquer software estatístico como o Excel para obter a equação da regressão linear, traçar o gráfico de dispersão e desenhar a linha de regressão.
Como funciona a análise de regressão?
A regressão linear consiste em encontrar a linha reta que melhor se ajusta através dos pontos. Defina uma variável dependente que você supõe ser influenciada por uma ou várias variáveis independentes. Colete o conjunto de dados para essas variáveis.
Exemplo 1: Vamos considerar os dados abaixo para a venda de carros usados.
| Idade do carro (em anos) | Preço (em dólares) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Olhando para os dados, podemos dizer que o preço do carro diminui com o aumento da idade do carro.
A fórmula para uma linha de regressão é Y = a + bX, deduza a e b usando as fórmulas abaixo
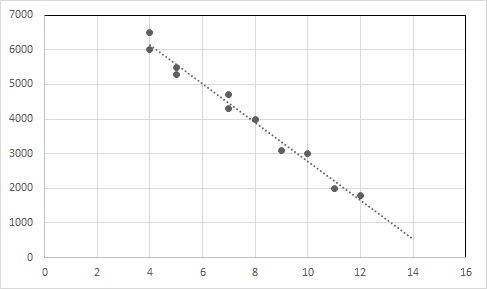
A equação de regressão linear para esta relação é Y = -557,62125 X + 8356,81293
Plote os pontos de dados e a linha de regressão em um gráfico.
Eixo X : Idade, Eixo Y : Preço
Exemplo2: John é um encanador. Ele cobra US$ 25 dólares como taxa de visita e US$ 35 como taxa de trabalho por hora. Uma equação linear que expressa a quantia total de dinheiro que John ganha por cada visita é y = 25 + 35x.
Por que a análise de regressão?