Ты выучишь:
Регрессионный анализ — это способ соотнесения переменных друг с другом. Переменные — это просто биты информации, которую мы собрали. Используя регрессионный анализ, мы можем найти закономерности в наших данных. Это позволяет нам делать прогнозы на основе наших данных. Статистическая регрессия — это метод, используемый для определения того, как на зависимую переменную влияют одна или несколько независимых переменных. С математической точки зрения статистическая регрессия отвечает на вопрос: как повлияет на значение Y (зависимая переменная) изменение значения X (независимой переменной)?
Например, мы хотим выяснить связь между возрастом и ценой подержанных автомобилей, проданных в прошлом году автодилером. Мы увидим отрицательную связь между этими двумя переменными. С возрастом автомобиля цены снижаются. В этом примере возраст автомобиля и цена автомобиля являются двумя переменными. Цена автомобиля зависит от возраста автомобиля. Мы хотим найти уравнение, которое наилучшим образом соответствует имеющимся у нас данным. Очень простая модель регрессионного анализа, которую мы можем использовать для нашего примера, называется линейной моделью , которая использует простое линейное уравнение для подгонки данных. Линейные уравнения при графическом отображении дают прямую линию.
Уравнение линейной регрессии или также известное как формула наклона имеет вид Y= a + bX, где Y — зависимая переменная (то есть переменная, которая идет по оси Y), X — независимая переменная (т. ось X), b — это наклон линии, а a — точка пересечения с осью y (значение y при x = 0).
Наклон линии — это значение, которое описывает скорость изменения между независимыми и зависимыми переменными. Наклон говорит нам, как зависимая переменная ( y ) изменяется в среднем на каждую единицу увеличения независимой ( x ) переменной. Y -перехват используется для описания зависимой переменной, когда независимая переменная равна нулю.
b>0 показывает положительную связь между двумя переменными.
Вы также можете использовать любое статистическое программное обеспечение, такое как Excel, чтобы получить уравнение линейной регрессии, построить точечную диаграмму и нарисовать линию регрессии.
Как работает регрессионный анализ?
Линейная регрессия заключается в поиске наиболее подходящей прямой линии, проходящей через точки. Определите зависимую переменную, на которую, как вы предполагаете, влияет одна или несколько независимых переменных. Соберите набор данных для этих переменных.
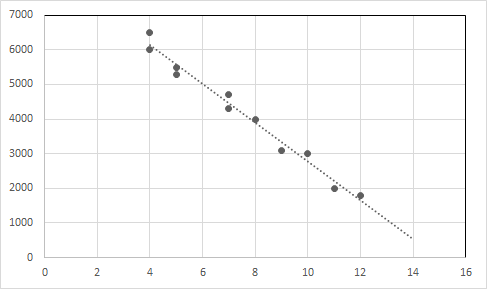
Пример 1: Рассмотрим приведенные ниже данные о продаже подержанных автомобилей.
| Возраст автомобиля (в годах) | Цена (в долларах) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 г. |
| 12 | 1800 |
Глядя на данные, мы можем сказать, что цена автомобиля снижается с увеличением возраста автомобиля.
Формула для линии регрессии: Y = a + bX, выведите a и b, используя приведенные ниже формулы.
Уравнение линейной регрессии для этой зависимости: Y = -557,62125 X + 8356,81293.
Постройте точки данных и линию регрессии на графике.
Ось X: возраст, ось Y: цена
Пример 2: Джон — сантехник. Он берет 25 долларов за посещение и 35 долларов за почасовую оплату. Линейное уравнение, выражающее общую сумму денег, которую Джон зарабатывает за каждое посещение, имеет вид y = 25 + 35x.
Почему регрессионный анализ?