Du kommer att lära dig:
Regressionsanalys är ett sätt att relatera variabler till varandra. Variabler är helt enkelt den information vi har samlat in. Genom att använda regressionsanalys kan vi hitta mönster i vår data. Det tillåter oss att göra förutsägelser baserat på vår data. Statistisk regression är en teknik som används för att bestämma hur en beroende variabel påverkas av en eller flera oberoende variabler. I matematiska termer svarar statistisk regression på frågan: Vad blir effekten på värdet av Y (den beroende variabeln) om värdet på X (den oberoende variabeln) ändras?
Till exempel - vi vill ta reda på sambandet mellan ålder och pris på begagnade bilar som såldes förra året av en bilhandlare. Vi kommer att se ett negativt samband mellan dessa två variabler. I takt med att bilåldern stiger sjunker priserna. I det här exemplet är bilålder och bilpris två variabler. Bilpriset är beroende av bilens ålder. Det vi vill hitta är en ekvation som bäst passar de data vi har. En mycket enkel regressionsanalysmodell som vi kan använda för vårt exempel kallas den linjära modellen , som använder en enkel linjär ekvation för att passa data. Linjära ekvationer när de ritas graf ger dig en rak linje.
Linjär regressionsekvation eller även igenkänd som lutningsformeln har formen Y= a + bX, där Y är den beroende variabeln (det är variabeln som går på Y-axeln), X är den oberoende variabeln (dvs den är plottad på X-axeln), b är linjens lutning och a är y-skärningen (värdet på y när x = 0).
Lutningen på en linje är ett värde som beskriver förändringshastigheten mellan de oberoende och beroende variablerna. Lutningen talar om för oss hur den beroende variabeln ( y ) förändras för varje en-enhetsökning i den oberoende ( x ) variabeln i genomsnitt. Y -avsnittet används för att beskriva den beroende variabeln när den oberoende variabeln är lika med noll.
b>0 visar ett positivt samband mellan de två variablerna.
Du kan också använda vilken statistisk programvara som helst som excel för att få ekvationen för linjär regression, för att plotta spridningsdiagrammet och rita regressionslinjen.
Hur fungerar regressionsanalys?
Linjär regression består av att hitta den räta linjen som passar bäst genom punkterna. Definiera en beroende variabel som du antar att den påverkas av en eller flera oberoende variabler. Samla datauppsättningen för dessa variabler.
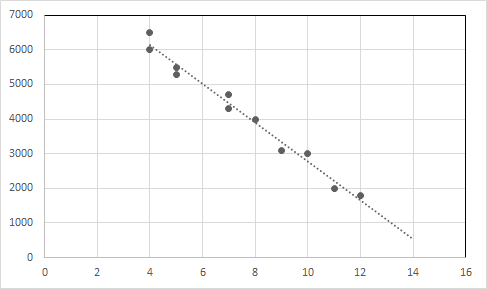
Exempel 1: Låt oss överväga nedanstående data för försäljningen av begagnade bilar.
| Bilens ålder (i år) | Pris (i dollar) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Om vi tittar på data kan vi säga att bilpriset minskar med stigande bilålder.
Formeln för en regressionslinje är Y= a + bX, härled a och b med nedanstående formler
Den linjära regressionsekvationen för detta förhållande är Y = -557,62125 X + 8356,81293
Rita datapunkterna och regressionslinjen i en graf.
X-axel : Ålder, Y-axel : Pris
Exempel 2: John är en rörmokare. Han debiterar $25 dollar som besöksavgift och $35 som hans timavgifter. En linjär ekvation som uttrycker den totala summan pengar John tjänar för varje besök är y = 25 + 35x.
Varför regressionsanalysen?