Utajifunza:
Uchambuzi wa urejeshi ni njia ya kuhusisha vigeuzo kwa kila kimoja. Vigezo ni sehemu ndogo tu za habari ambazo tumekusanya. Kwa kutumia uchanganuzi wa urejeshaji, tunaweza kupata ruwaza katika data yetu. Inaturuhusu kufanya ubashiri kulingana na data yetu. Urejeshaji wa Kitakwimu ni mbinu inayotumiwa kubainisha jinsi kigeu tegemezi kinavyoathiriwa na kigezo kimoja au zaidi huru. Kwa maneno ya kihesabu Regression ya Takwimu hujibu swali: Je, itakuwa na athari gani kwa thamani ya Y (kigeu tegemezi) ikiwa thamani ya X (kigeuzi huru) kitabadilishwa?
Kwa mfano - tunataka kujua uhusiano kati ya umri na bei ya magari yaliyotumika yaliyouzwa mwaka jana na muuzaji wa magari. Tutaona uhusiano mbaya kati ya vigezo hivi viwili. Kadiri umri wa magari unavyoongezeka bei hupungua. Katika mfano huu, umri wa gari na bei ya gari ni vigezo viwili. Bei ya gari inategemea umri wa gari. Tunachotaka kupata ni mlinganyo unaolingana vyema na data tuliyo nayo. Mfano rahisi sana wa uchanganuzi wa urejeshi ambao tunaweza kutumia kwa mfano wetu unaitwa mfano wa mstari , ambao hutumia mlinganyo rahisi wa mstari kutoshea data. Milinganyo ya mstari wakati imechorwa hukupa mstari ulionyooka.
Mlinganyo wa urejeshaji wa mstari au unaotambuliwa pia kama fomula ya mteremko ina fomu Y= a + bX, ambapo Y ni kigezo tegemezi (hicho ni kigezo kinachoendelea kwenye mhimili wa Y), X ni kigezo huru (yaani kimepangwa kwenye mhimili wa Y). X-mhimili), b ni mteremko wa mstari na a ni y-katiza (thamani ya y wakati x = 0).
Mteremko wa mstari ni thamani inayoelezea kiwango cha mabadiliko kati ya vigezo huru na tegemezi. Mteremko hutuambia jinsi tofauti tegemezi ( y ) inavyobadilika kwa kila ongezeko la kitengo kimoja katika utofauti unaojitegemea ( x ), kwa wastani. y -intercept hutumika kuelezea kigezo tegemezi wakati kigezo huru kinalingana na sufuri.
b>0 inaonyesha uhusiano chanya kati ya vigezo viwili.
Unaweza pia kutumia programu yoyote ya takwimu kama excel kupata mlinganyo wa rejista ya mstari, kupanga chati ya kutawanya, na kuchora mstari wa rejista.
Uchambuzi wa rejista hufanyaje kazi?
Urejeshaji wa mstari unajumuisha kupata laini iliyonyooka inayofaa zaidi kupitia alama. Bainisha kigezo tegemezi ambacho unakisia kuathiriwa na kigezo kimoja au kadhaa huru. Kusanya seti ya data kwa vigeu hivi.
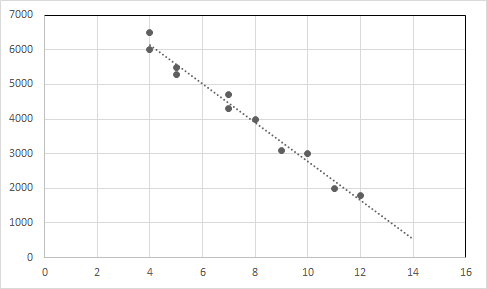
Mfano 1: Hebu tuzingatie data iliyo hapa chini ya uuzaji wa magari yaliyotumika.
| Umri wa gari (katika miaka) | Bei (kwa dola) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Kuangalia data tunaweza kusema kwamba bei ya gari inapungua kwa ongezeko la umri wa gari.
Fomula ya laini ya rejista ni Y= a + bX, pata a na b kwa kutumia fomula zilizo hapa chini
Mlinganyo wa urejeshaji wa mstari wa uhusiano huu ni Y = -557.62125 X + 8356.81293
Panga vidokezo vya data na mstari wa rejista kwenye grafu.
Mhimili wa X : Umri, mhimili wa Y: Bei
Mfano2: John ni fundi bomba. Anatoza dola 25 kama malipo ya kutembelea na $35 kama malipo yake ya kufanya kazi kwa saa. Mlinganyo wa mstari unaoonyesha jumla ya pesa anazopata John kwa kila ziara ni y = 25 + 35x.
Kwa nini uchanganuzi wa kurudi nyuma?