คุณจะได้เรียนรู้:
การวิเคราะห์การถดถอย เป็นวิธีการเชื่อมโยงตัวแปรเข้าด้วยกัน ตัวแปรเป็นเพียงส่วนเล็กๆ ของข้อมูลที่เรารวบรวมไว้ โดยใช้การวิเคราะห์การถดถอย เราสามารถหารูปแบบในข้อมูลของเราได้ ช่วยให้เราสามารถคาดการณ์ได้จากข้อมูลของเรา การถดถอยทางสถิติเป็นเทคนิคที่ใช้ในการพิจารณาว่าตัวแปรตามได้รับผลกระทบจากตัวแปรอิสระตั้งแต่หนึ่งตัวขึ้นไปอย่างไร ในแง่คณิตศาสตร์ การถดถอยทางสถิติตอบคำถาม: อะไรจะเกิดขึ้นกับค่าของ Y (ตัวแปรตาม) ถ้าค่าของ X (ตัวแปรอิสระ) เปลี่ยนไป?
ตัวอย่างเช่น เราต้องการค้นหาความสัมพันธ์ระหว่างอายุและราคาของรถยนต์มือสองที่ขายเมื่อปีที่แล้วโดยตัวแทนจำหน่ายรถยนต์ เราจะเห็นความสัมพันธ์เชิงลบระหว่างสองตัวแปรนี้ พออายุรถมากขึ้นราคาก็ลง ในตัวอย่างนี้ อายุรถและราคารถเป็นสองตัวแปร ราคารถขึ้นอยู่กับอายุรถ สิ่งที่เราต้องการค้นหาคือสมการที่เหมาะกับข้อมูลที่เรามีมากที่สุด แบบจำลองการวิเคราะห์การถดถอยอย่างง่ายที่เราสามารถใช้สำหรับตัวอย่างของเราเรียกว่า แบบจำลองเชิงเส้น ซึ่งใช้สมการเชิงเส้นอย่างง่ายเพื่อให้พอดีกับข้อมูล สมการเชิงเส้นเมื่อวาดกราฟจะให้เส้นตรง
สมการถดถอยเชิงเส้นหรือที่เรียกว่า สูตรความชัน มีรูปแบบ Y= a + bX โดยที่ Y คือตัวแปรตาม (นั่นคือตัวแปรที่อยู่บนแกน Y) X คือตัวแปรอิสระ (กล่าวคือ มันถูกลงจุดบน แกน X), b คือความชันของเส้นตรง และ a คือจุดตัดแกน y(ค่าของ y เมื่อ x = 0)
ความชันของเส้น เป็นค่าที่อธิบายอัตราการเปลี่ยนแปลงระหว่างตัวแปรอิสระและตัวแปรตาม ความชัน บอกเราว่าตัวแปรตาม ( y ) เปลี่ยนแปลงอย่างไรสำหรับทุก ๆ หนึ่งหน่วยที่เพิ่มขึ้นในตัวแปรอิสระ ( x ) โดยเฉลี่ย y -intercept ใช้เพื่ออธิบายตัวแปรตามเมื่อตัวแปรอิสระมีค่าเท่ากับศูนย์
b>0 แสดงความสัมพันธ์เชิงบวกระหว่างตัวแปรทั้งสอง
คุณยังสามารถใช้ซอฟต์แวร์ทางสถิติใดๆ เช่น excel เพื่อรับสมการสำหรับการถดถอยเชิงเส้น วางแผนแผนภูมิกระจาย และวาดเส้นการถดถอย
การวิเคราะห์การถดถอยทำงานอย่างไร
การถดถอยเชิงเส้นประกอบด้วยการหาเส้นตรงที่เหมาะสมที่สุดผ่านจุดต่างๆ กำหนดตัวแปรตามที่คุณตั้งสมมติฐานว่าได้รับอิทธิพลจากตัวแปรอิสระหนึ่งตัวหรือหลายตัว รวบรวมชุดข้อมูลสำหรับตัวแปรเหล่านี้
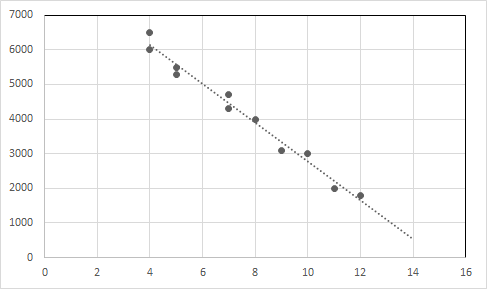
ตัวอย่างที่ 1: ลองพิจารณาข้อมูลด้านล่างสำหรับการขายรถมือสอง
| อายุรถ (ปี) | ราคา (เป็นดอลลาร์) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2543 |
| 12 | 1800 |
เมื่อดูข้อมูลเราสามารถพูดได้ว่าราคารถยนต์ลดลงตามอายุรถยนต์ที่เพิ่มขึ้น
สูตรสำหรับเส้นถดถอยคือ Y= a + bX หาค่า a และ b โดยใช้สูตรด้านล่าง
สมการถดถอยเชิงเส้นสำหรับความสัมพันธ์นี้คือ Y = -557.62125 X + 8356.81293
เขียนจุดข้อมูลและเส้นการถดถอยในกราฟ
แกน X : อายุ แกน Y : ราคา
ตัวอย่างที่ 2: จอห์นเป็นช่างประปา เขาเรียกเก็บเงิน 25 ดอลลาร์เป็นค่าเยี่ยมและ 35 ดอลลาร์เป็นค่าทำงานรายชั่วโมง สมการเชิงเส้นที่แสดงจำนวนเงินทั้งหมดที่จอห์นได้รับสำหรับการเข้าชมแต่ละครั้งคือ y = 25 + 35x
ทำไมต้องวิเคราะห์การถดถอย?