Öğreneceksiniz:
Regresyon analizi , değişkenleri birbiriyle ilişkilendirmenin bir yoludur. Değişkenler basitçe topladığımız bilgi parçalarıdır. Regresyon analizini kullanarak verilerimizdeki kalıpları bulabiliriz. Verilerimize dayanarak tahminler yapmamızı sağlar. İstatistiksel Regresyon, bir bağımlı değişkenin bir veya daha fazla bağımsız değişkenden nasıl etkilendiğini belirlemek için kullanılan bir tekniktir. Matematiksel terimlerle İstatistiksel Regresyon şu soruyu yanıtlar: X'in (bağımsız değişken) değeri değiştirilirse Y'nin (bağımlı değişken) değeri üzerindeki etkisi ne olur?
Örneğin, geçen yıl bir araba satıcısı tarafından satılan ikinci el arabaların yaşı ile fiyatı arasındaki ilişkiyi bulmak istiyoruz. Bu iki değişken arasında negatif bir ilişki göreceğiz. Araba yaşı arttıkça fiyatlar düşüyor. Bu örnekte araba yaşı ve araba fiyatı iki değişkendir. Araba fiyatı araba yaşına bağlıdır. Bulmak istediğimiz şey, sahip olduğumuz verilere en iyi uyan denklemdir. Örneğimiz için kullanabileceğimiz çok basit bir regresyon analizi modeline, verileri sığdırmak için basit bir doğrusal denklem kullanan doğrusal model denir. Doğrusal denklemler grafiklendirildiğinde size düz bir çizgi verir.
Doğrusal regresyon denklemi veya eğim formülü olarak da bilinen Y= a + bX biçimindedir, burada Y bağımlı değişkendir (bu, Y ekseni üzerinde giden değişkendir), X bağımsız değişkendir (örn. X ekseni), b çizginin eğimidir ve a y-kesme noktasıdır ( x = 0 olduğunda y'nin değeri).
Bir doğrunun eğimi , bağımsız ve bağımlı değişkenler arasındaki değişim oranını tanımlayan bir değerdir. Eğim , ortalama olarak bağımsız ( x ) değişkendeki her bir birimlik artış için bağımlı değişkenin ( y ) nasıl değiştiğini anlatır. Bağımsız değişken sıfıra eşit olduğunda bağımlı değişkeni tanımlamak için y -intercept kullanılır.
b>0, iki değişken arasında pozitif bir ilişkiyi gösterir.
Doğrusal regresyon denklemini elde etmek, dağılım grafiğini çizmek ve regresyon çizgisini çizmek için excel gibi herhangi bir istatistik yazılımını da kullanabilirsiniz.
Regresyon analizi nasıl çalışır?
Doğrusal regresyon, noktalardan geçen en uygun düz çizgiyi bulmayı içerir. Bir veya birkaç bağımsız değişkenden etkilendiğini varsaydığınız bir bağımlı değişken tanımlayın. Bu değişkenler için veri kümesini toplayın.
Örnek 1: İkinci el araba satışı için aşağıdaki verileri inceleyelim.
| Araba Yaşı (yıl olarak) | Fiyat (dolar olarak) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Verilere baktığımızda, araba yaşının artmasıyla birlikte araba fiyatının düştüğünü söyleyebiliriz.
Bir regresyon çizgisinin formülü Y= a + bX'tir, aşağıdaki formülleri kullanarak a ve b'yi türetin
Bu ilişki için doğrusal regresyon denklemi Y = -557.62125 X + 8356.81293'tür.
Veri noktalarını ve regresyon çizgisini bir grafikte çizin.
X ekseni : Yaş, Y ekseni : Fiyat
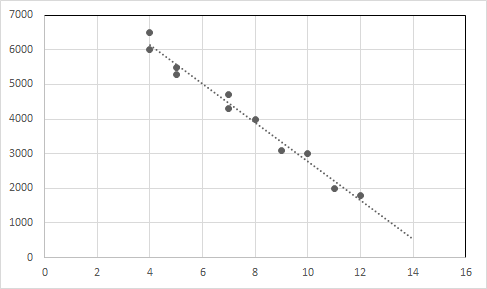
Örnek2: John bir tesisatçıdır. Ziyaret ücreti olarak 25 dolar ve saatlik çalışma ücreti olarak 35 dolar alıyor. John'un her ziyaret için kazandığı toplam parayı ifade eden doğrusal bir denklem y = 25 + 35x'tir.
Neden regresyon analizi?