Back to the topics list

статистична регресія

Ти навчишся:

• Що таке статистична регресія?
• Рівняння лінійної регресії та його виведення
• Використання регресійного аналізу

Регресійний аналіз – це спосіб встановлення зв’язків між змінними. Змінні – це просто фрагменти інформації, яку ми зібрали. Використовуючи регресійний аналіз, ми можемо знайти закономірності в наших даних. Це дозволяє нам робити прогнози на основі наших даних. Статистична регресія – це техніка, яка використовується для визначення того, як на залежну змінну впливає одна або кілька незалежних змінних. У математичних термінах статистична регресія відповідає на запитання: який вплив матиме на значення Y (залежна змінна), якщо значення X (незалежна змінна) буде змінено?

Наприклад, ми хочемо з'ясувати зв'язок між віком і ціною вживаних автомобілів, проданих минулого року автодилером. Ми побачимо негативну залежність між цими двома змінними. Зі збільшенням віку автомобіля ціни падають. У цьому прикладі вік автомобіля та ціна автомобіля є двома змінними. Ціна автомобіля залежить від віку автомобіля. Ми хочемо знайти рівняння, яке найкраще відповідає наявним у нас даним. Дуже проста модель регресійного аналізу, яку ми можемо використати для нашого прикладу, називається лінійною моделлю , яка використовує просте лінійне рівняння для підгонки даних. Лінійні рівняння в графіку дають вам пряму лінію.

Рівняння лінійної регресії або також відоме як формула нахилу має вигляд Y= a + bX, де Y — залежна змінна (це змінна, яка проходить по осі Y), X — незалежна змінна (тобто вона зображена на графіку вісь X), b – кут нахилу лінії, a – точка перетину y (значення y , коли x = 0).

Нахил лінії — це значення, яке описує швидкість зміни між незалежною та залежною змінними. Нахил показує нам, як залежна змінна ( y ) змінюється в середньому для кожного збільшення незалежної змінної ( x ) на одну одиницю. Перетин y використовується для опису залежної змінної, коли незалежна змінна дорівнює нулю.

\(a = \frac{(\Sigma y)(\Sigma x^2) - (\Sigma x) (\Sigma xy)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

\(b = \frac{n(\Sigma xy) - (\Sigma x) (\Sigma y)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

b>0 показує позитивний зв'язок між двома змінними.

Ви також можете використовувати будь-яке статистичне програмне забезпечення, наприклад Excel, щоб отримати рівняння лінійної регресії, побудувати точкову діаграму та накреслити лінію регресії.

Як працює регресійний аналіз?
Лінійна регресія полягає у знаходженні найкращої прямої лінії, що проходить через точки. Визначте залежну змінну, на яку, за вашою гіпотезою, впливає одна або декілька незалежних змінних. Зберіть набір даних для цих змінних.
Приклад 1. Розглянемо наведені нижче дані щодо продажу вживаних автомобілів.

Дивлячись на дані, можна сказати, що ціна автомобіля знижується зі збільшенням віку автомобіля.

Формула для лінії регресії: Y= a + bX, виведіть a і b за допомогою наведених нижче формул

\(a = \frac{(\Sigma y)(\Sigma x^2) - (\Sigma x) (\Sigma xy)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

\(b = \frac{n(\Sigma xy) - (\Sigma x) (\Sigma y)} {n(\Sigma x^2) - (\Sigma x)^2 }\)

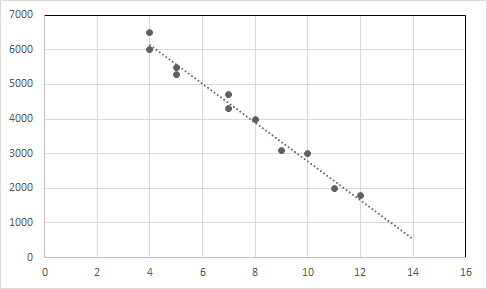
Рівняння лінійної регресії для цього співвідношення: Y = -557,62125 X + 8356,81293

Нанесіть точки даних і лінію регресії на графік.

Вісь X: вік, вісь Y: ціна

Приклад 2: Джон – сантехнік. Він бере 25 доларів за відвідування та 35 доларів за погодинну роботу. Лінійне рівняння, яке виражає загальну суму грошей, яку Джон заробляє за кожен візит, дорівнює y = 25 + 35x.

Чому регресійний аналіз?

• Регресія може бути використана для визначення сили впливу незалежної змінної (змінних) на залежну змінну. Приклад: яка сила зв’язку між дозою та ефектом, витратами на продаж і маркетинг або віком і доходом.
• Його можна використовувати для прогнозування наслідків або впливу змін. Тобто регресійний аналіз допомагає нам зрозуміти, наскільки залежна змінна змінюється при зміні однієї чи кількох незалежних змінних. Приклад. Скільки додаткового доходу від продажу я отримаю за кожні додаткові 1000 доларів США, витрачених на маркетинг?
• Регресійний аналіз передбачає тенденції та майбутні значення. Регресійний аналіз можна використовувати для отримання точкових оцінок. Наприклад, якою буде ціна на золото через 6 місяців?