آپ سیکھیں گے:
رجعت کا تجزیہ متغیرات کو ایک دوسرے سے جوڑنے کا ایک طریقہ ہے۔ متغیرات صرف معلومات کے بٹس ہیں جو ہم نے جمع کیے ہیں۔ رجعت تجزیہ کا استعمال کرکے، ہم اپنے ڈیٹا میں پیٹرن تلاش کرسکتے ہیں۔ یہ ہمیں اپنے ڈیٹا کی بنیاد پر پیشین گوئیاں کرنے کی اجازت دیتا ہے۔ شماریاتی رجعت ایک تکنیک ہے جس کا استعمال اس بات کا تعین کرنے کے لیے کیا جاتا ہے کہ ایک منحصر متغیر، ایک یا زیادہ آزاد متغیرات سے کیسے متاثر ہوتا ہے۔ ریاضیاتی اصطلاحات میں شماریاتی رجعت اس سوال کا جواب دیتا ہے: اگر X (آزاد متغیر) کی قدر کو تبدیل کیا جائے تو Y (انحصار متغیر) کی قدر پر کیا اثر پڑے گا؟
مثال کے طور پر - ہم کار ڈیلر کے ذریعہ پچھلے سال فروخت کی گئی استعمال شدہ کاروں کی عمر اور قیمت کے درمیان تعلق معلوم کرنا چاہتے ہیں۔ ہم ان دو متغیرات کے درمیان ایک منفی تعلق دیکھیں گے۔ جیسے جیسے گاڑی کی عمر بڑھتی ہے قیمتیں کم ہوتی جاتی ہیں۔ اس مثال میں، کار کی عمر اور کار کی قیمت دو متغیر ہیں۔ کار کی قیمت کار کی عمر پر منحصر ہے۔ جو ہم تلاش کرنا چاہتے ہیں وہ ایک مساوات ہے جو ہمارے پاس موجود ڈیٹا کو بہترین طریقے سے فٹ کرتی ہے۔ ایک بہت ہی آسان ریگریشن تجزیہ ماڈل جسے ہم اپنی مثال کے لیے استعمال کر سکتے ہیں اسے لکیری ماڈل کہا جاتا ہے، جو ڈیٹا کو فٹ کرنے کے لیے ایک سادہ لکیری مساوات کا استعمال کرتا ہے۔ لکیری مساوات جب گراف کی جاتی ہیں تو آپ کو سیدھی لکیر دیتی ہیں۔
لکیری ریگریشن مساوات یا ڈھلوان کے فارمولے کے طور پر بھی پہچانا جاتا ہے جس کی شکل Y= a + bX ہے، جہاں Y منحصر متغیر ہے (یہ وہ متغیر ہے جو Y-axis پر جاتا ہے)، X آزاد متغیر ہے (یعنی اس پر پلاٹ کیا گیا ہے X-axis)، b لائن کی ڈھلوان ہے اور a y-انٹرسیپٹ ہے ( y کی قدر جب x = 0)۔
لائن کی ڈھلوان ایک قدر ہے جو آزاد اور منحصر متغیر کے درمیان تبدیلی کی شرح کو بیان کرتی ہے۔ ڈھلوان ہمیں بتاتی ہے کہ منحصر متغیر ( y ) اوسطاً آزاد ( x ) متغیر میں ہر ایک یونٹ کے اضافے کے لیے کیسے بدلتا ہے۔ y -intercept کا استعمال منحصر متغیر کی وضاحت کے لیے کیا جاتا ہے جب آزاد متغیر صفر کے برابر ہوتا ہے۔
b>0 دو متغیرات کے درمیان ایک مثبت تعلق کو ظاہر کرتا ہے۔
آپ کسی بھی شماریاتی سافٹ ویئر کا استعمال بھی کر سکتے ہیں جیسے کہ ایکسل لکیری ریگریشن کی مساوات حاصل کرنے کے لیے، سکیٹر چارٹ کو پلاٹ کرنے کے لیے، اور رجعت کی لکیر کھینچنے کے لیے۔
رجعت کا تجزیہ کیسے کام کرتا ہے؟
لکیری ریگریشن پوائنٹس کے ذریعے بہترین فٹنگ سیدھی لائن تلاش کرنے پر مشتمل ہے۔ ایک منحصر متغیر کی وضاحت کریں جس کے بارے میں آپ ایک یا متعدد آزاد متغیرات سے متاثر ہونے کا قیاس کرتے ہیں۔ ان متغیرات کے لیے ڈیٹاسیٹ جمع کریں۔
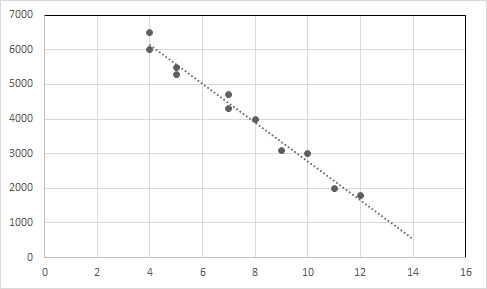
مثال 1: آئیے استعمال شدہ کار کی فروخت کے لیے درج ذیل ڈیٹا پر غور کریں۔
| کار کی عمر (سالوں میں) | قیمت (ڈالر میں) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
اعداد و شمار کو دیکھ کر ہم کہہ سکتے ہیں کہ کار کی عمر میں اضافے کے ساتھ کار کی قیمت کم ہوتی ہے۔
ریگریشن لائن کا فارمولا Y= a + bX ہے، ذیل کے فارمولوں کا استعمال کرتے ہوئے a اور b حاصل کریں
اس تعلق کے لیے لکیری ریگریشن مساوات Y = -557.62125 X + 8356.81293 ہے
ڈیٹا پوائنٹس اور ریگریشن لائن کو گراف میں پلاٹ کریں۔
ایکس محور : عمر، وائی محور : قیمت
مثال 2: جان ایک پلمبر ہے۔ وہ $25 ڈالر وزٹنگ چارج کے طور پر اور $35 اپنے گھنٹہ وار ورکنگ چارجز کے طور پر لیتا ہے۔ ایک لکیری مساوات جو جان کی ہر وزٹ کے لیے کمائی جانے والی کل رقم کو ظاہر کرتی ہے y = 25 + 35x ہے۔
رجعت کا تجزیہ کیوں؟