Siz o'rganasiz:
Regressiya tahlili o'zgaruvchilarni bir-biriga bog'lash usulidir. O'zgaruvchilar shunchaki biz to'plagan ma'lumotlarning bir qismidir. Regressiya tahlilidan foydalanib, biz ma'lumotlarimizdagi naqshlarni topishimiz mumkin. Bu bizga ma'lumotlarimiz asosida bashorat qilish imkonini beradi. Statistik regressiya - bu qaram o'zgaruvchiga bir yoki bir nechta mustaqil o'zgaruvchilar qanday ta'sir qilishini aniqlash uchun ishlatiladigan usul. Matematik nuqtai nazardan Statistik regressiya savolga javob beradi: X (mustaqil o'zgaruvchi) qiymati o'zgartirilsa, Y (qaram o'zgaruvchi) qiymatiga qanday ta'sir qiladi?
Masalan, biz avtosalon tomonidan o'tgan yili sotilgan eski avtomobillarning yoshi va narxi o'rtasidagi bog'liqlikni aniqlamoqchimiz. Biz bu ikki o'zgaruvchi o'rtasida salbiy munosabatni ko'ramiz. Avtomobilning yoshi oshgani sayin narxlar pasayadi. Ushbu misolda avtomobil yoshi va avtomobil narxi ikkita o'zgaruvchidir. Avtomobil narxi avtomobil yoshiga bog'liq. Biz topmoqchi bo'lgan narsa bizda mavjud bo'lgan ma'lumotlarga eng mos keladigan tenglamadir. Bizning misolimiz uchun foydalanishimiz mumkin bo'lgan juda oddiy regressiya tahlili modeli chiziqli model deb ataladi, u ma'lumotlarni moslashtirish uchun oddiy chiziqli tenglamadan foydalanadi. Grafik chizilgan chiziqli tenglamalar sizga to'g'ri chiziq beradi.
Chiziqli regressiya tenglamasi yoki qiyalik formulasi sifatida ham tan olingan Y= a + bX ko'rinishga ega, bu erda Y - bog'liq o'zgaruvchi (ya'ni Y o'qi bo'yicha ketadigan o'zgaruvchi), X - mustaqil o'zgaruvchi (ya'ni, u grafada chizilgan). X-o'qi), b - chiziqning qiyaligi va a - y-kesimi ( x = 0 bo'lganda y ning qiymati).
Chiziq qiyaligi mustaqil va bog'liq o'zgaruvchilar orasidagi o'zgarish tezligini tavsiflovchi qiymatdir. Nishab bizga mustaqil ( x ) o'zgaruvchidagi har bir birlik o'sish uchun bog'liq o'zgaruvchining ( y ) o'rtacha qanday o'zgarishini aytadi. y -kesishmasi mustaqil o'zgaruvchi nolga teng bo'lganda, qaram o'zgaruvchini tavsiflash uchun ishlatiladi.
b>0 ikki o'zgaruvchi o'rtasidagi ijobiy munosabatni ko'rsatadi.
Chiziqli regressiya uchun tenglamani olish, tarqalish diagrammasini tuzish va regressiya chizig'ini chizish uchun Excel kabi har qanday statistik dasturlardan ham foydalanishingiz mumkin.
Regressiya tahlili qanday ishlaydi?
Chiziqli regressiya nuqtalar orqali eng mos keladigan to'g'ri chiziqni topishdan iborat. Bir yoki bir nechta mustaqil o'zgaruvchilar ta'sirida bo'lgan deb taxmin qilgan qaram o'zgaruvchini aniqlang. Ushbu o'zgaruvchilar uchun ma'lumotlar to'plamini to'plang.
1-misol: Ishlatilgan avtomobillarni sotish bo'yicha quyidagi ma'lumotlarni ko'rib chiqamiz.
| Avtomobil yoshi (yillarda) | Narxi (dollar bilan) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Ma'lumotlarga nazar tashlaydigan bo'lsak, shuni aytishimiz mumkinki, avtomobil narxi avtomobil yoshi o'sishi bilan pasayadi.
Regressiya chizig'i formulasi Y= a + bX bo'lib, quyidagi formulalar yordamida a va b hosil qiling
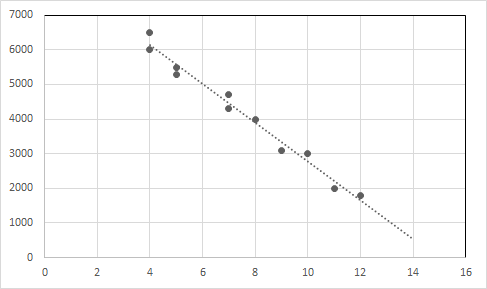
Bu munosabat uchun chiziqli regressiya tenglamasi Y = -557,62125 X + 8356,81293
Grafikda ma'lumotlar nuqtalari va regressiya chizig'ini chizing.
X o'qi : Yosh, Y o'qi : Narx
2-misol: Jon chilangar. U tashrif uchun 25 dollar va soatlik ish haqi sifatida 35 dollar oladi. Jon har bir tashrif uchun oladigan umumiy pul miqdorini ifodalovchi chiziqli tenglama y = 25 + 35x.
Nima uchun regressiya tahlili kerak?