Bạn sẽ học:
Phân tích hồi quy là một cách liên kết các biến với nhau. Các biến chỉ đơn giản là các bit thông tin chúng tôi đã thu thập. Bằng cách sử dụng phân tích hồi quy, chúng tôi có thể tìm thấy các mẫu trong dữ liệu của mình. Nó cho phép chúng tôi đưa ra dự đoán dựa trên dữ liệu của chúng tôi. Hồi quy thống kê là một kỹ thuật được sử dụng để xác định cách một biến phụ thuộc bị ảnh hưởng bởi một hoặc nhiều biến độc lập. Về mặt toán học, Hồi quy thống kê trả lời câu hỏi: Điều gì sẽ tác động đến giá trị của Y (biến phụ thuộc) nếu giá trị của X (biến độc lập) bị thay đổi?
Ví dụ: chúng tôi muốn tìm hiểu mối quan hệ giữa tuổi và giá của những chiếc ô tô đã qua sử dụng được bán vào năm ngoái bởi một đại lý ô tô. Chúng ta sẽ thấy một mối quan hệ tiêu cực giữa hai biến này. Khi tuổi xe tăng giá đi xuống. Trong ví dụ này, tuổi xe và giá xe là hai biến. Giá xe phụ thuộc vào tuổi xe. Những gì chúng tôi muốn tìm là một phương trình phù hợp nhất với dữ liệu mà chúng tôi có. Một mô hình phân tích hồi quy rất đơn giản mà chúng ta có thể sử dụng cho ví dụ của mình được gọi là mô hình tuyến tính , sử dụng một phương trình tuyến tính đơn giản để điều chỉnh dữ liệu. Các phương trình tuyến tính khi vẽ đồ thị cho bạn một đường thẳng.
Phương trình hồi quy tuyến tính hay còn gọi là công thức hệ số góc có dạng Y= a + bX, trong đó Y là biến phụ thuộc (tức là biến nằm trên trục Y), X là biến độc lập (tức là được vẽ trên trục Y). trục X), b là hệ số góc của đường thẳng và a là tung độ gốc của y (giá trị của y khi x = 0).
Độ dốc của một đường là một giá trị mô tả tốc độ thay đổi giữa các biến độc lập và biến phụ thuộc. Hệ số góc cho chúng ta biết trung bình biến phụ thuộc ( y ) thay đổi như thế nào đối với mỗi lần tăng một đơn vị của biến độc lập ( x ). Y -intercept được sử dụng để mô tả biến phụ thuộc khi biến độc lập bằng 0.
b>0 cho thấy mối quan hệ tích cực giữa hai biến.
Bạn cũng có thể sử dụng bất kỳ phần mềm thống kê nào như excel để lấy phương trình hồi quy tuyến tính, vẽ biểu đồ phân tán và vẽ đường hồi quy.
Phân tích hồi quy hoạt động như thế nào?
Hồi quy tuyến tính bao gồm việc tìm đường thẳng phù hợp nhất qua các điểm. Xác định một biến phụ thuộc mà bạn đưa ra giả thuyết bị ảnh hưởng bởi một hoặc một số biến độc lập. Thu thập tập dữ liệu cho các biến này.
Ví dụ 1: Hãy xem xét dữ liệu dưới đây cho việc bán ô tô đã qua sử dụng.
| Tuổi xe (tính bằng năm) | Giá (tính bằng đô la) |
| 4 | 6500 |
| 4 | 6000 |
| 5 | 5500 |
| 5 | 5300 |
| 7 | 4700 |
| 7 | 4300 |
| số 8 | 4000 |
| 9 | 3100 |
| 10 | 3000 |
| 11 | 2000 |
| 12 | 1800 |
Nhìn vào dữ liệu, chúng ta có thể nói rằng giá xe giảm khi tuổi xe tăng.
Công thức cho đường hồi quy là Y= a + bX, lấy a và b bằng các công thức bên dưới
Phương trình hồi quy tuyến tính cho mối quan hệ này là Y = -557,62125 X + 8356,81293
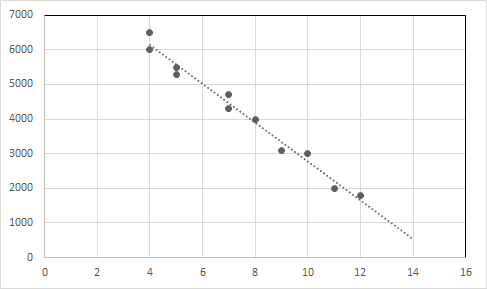
Vẽ các điểm dữ liệu và đường hồi quy trong biểu đồ.
Trục X : Tuổi, Trục Y : Giá
Ví dụ2: John là thợ sửa ống nước. Anh ta tính 25 đô la phí thăm viếng và 35 đô la phí làm việc theo giờ. Một phương trình tuyến tính biểu thị tổng số tiền John kiếm được cho mỗi lần truy cập là y = 25 + 35x.
Tại sao phải phân tích hồi quy?