سوف تتعلم:
التكاملات مع المشتقات هي العناصر الأساسية في حساب التفاضل والتكامل. تسمى عملية حساب التكامل بالتكامل ويطلق على الحساب التقريبي للتكامل اسم التكامل العددي.
هناك فئتان من التكاملات - التكامل المحدد (مثل 5) والتكاملات غير المحددة ، والتي لها حدود صغرى وأعلى مثل \(\int_a^bf(x) \cdot dx\) .
ما هو انتجرال؟
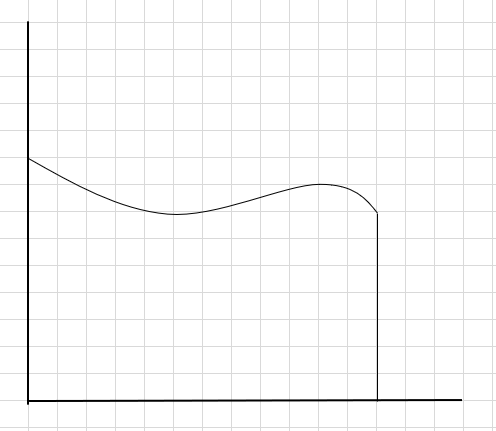
لنفترض أنه يتعين علينا إيجاد المنطقة الواقعة أسفل المنحنى ومحور x أعلاه.
تتمثل إحدى طرق القيام بذلك في تقسيم المنطقة إلى أربعة أجزاء ثم رسم مستطيل (باستخدام خط المقطع هذا) بحيث تلامس الزاوية اليمنى العليا لكل مستطيل المنحنى (كما هو موضح أدناه)
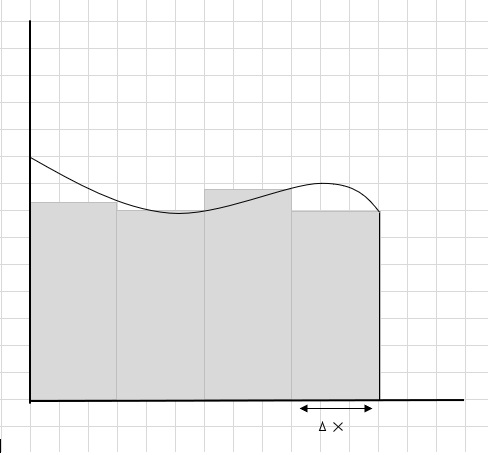
مجموع مساحة هذه المقاطع المستطيلة هو المساحة المقدرة أسفل هذا المنحنى. \(\Delta x \) هو عرض المستطيلات / الشرائح. ما رأيك في المساحة المقدرة؟
يتم فقدان جزء كبير من المنحنى ويتم أخذ بعض الأجزاء الإضافية في الاعتبار أثناء حساب مساحة منطقة المنحنى هذه. تسجيل الوصول أسفل الصورة يمثل المنطقة الرمادية الداكنة المفقودة وأجزاء إضافية.
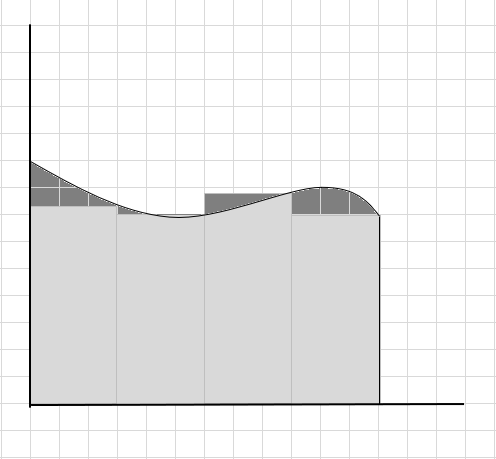
يمكننا القول أن هذا تقدير ضعيف لمساحة المنطقة المنحنية لأن المستطيلات لا تتناسب تمامًا مع المنحنى. دعنا نقسم المنطقة الواقعة تحت هذا المنحنى إلى أجزاء أصغر.
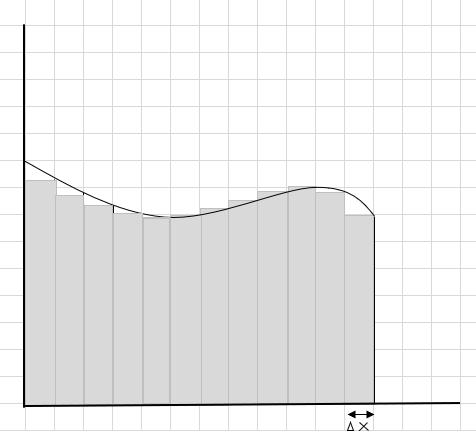
يمكنك أن ترى أن هذه المستطيلات تتلاءم مع المنطقة المنحنية بشكل أفضل من المقاطع المستطيلة الأكبر. دعنا نحاول تقسيم هذه المنطقة المنحنية إلى شرائح / شرائح أصغر ونحاول تحديد المنطقة الواقعة أسفل المنحنى.
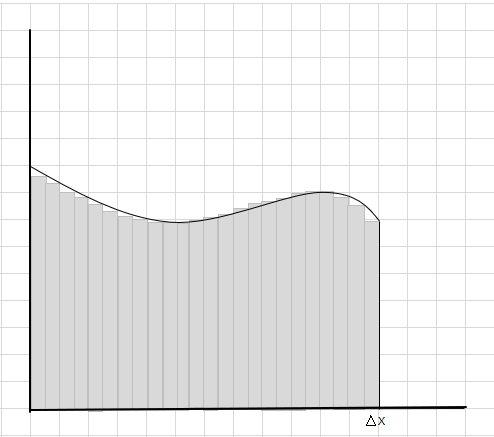
يتم تقليل الأجزاء المفقودة والأجزاء الإضافية تدريجيًا وتكون المستطيلات مناسبة بشكل أفضل داخل منطقة المنحنى. يمكننا أن نستنتج أن مجموع مساحة كل هذه المستطيلات يعطي تقديرًا جيدًا للمساحة الواقعة أسفل المنحنى. أو بعبارة أخرى ، يمكننا القول عندما تقترب الشرائح من الصفر ، تقترب الإجابة من الإجابة الصحيحة. نكتب الآن dx لـ \(\Delta x\) لنعني أن العرض يقترب من الصفر.
لنشتق صيغة حساب التفاضل والتكامل هنا:
لنفترض أننا بحاجة إلى إيجاد المساحة الواقعة أسفل هذا المنحنى بين النقطتين أ وب: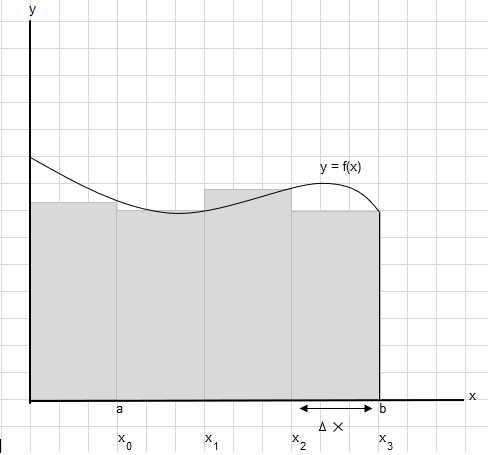
قسّم المنطقة الواقعة بين a و b إلى أجزاء متساوية بحيث يكون عرض كل مستطيل \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
يمكن كتابة مجموع مساحة هذه المستطيلات كـ \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
يمكننا الحصول على تقريب أفضل للمنطقة حيث أن \(\Delta x \) يصبح أصغر أو بعبارة أخرى عندما يزداد عدد المقاطع. لذلك \(\Delta x \) يصبح أرق وأرق ويصبح n أكبر وأكبر. فكرة الحصول على تقريب أفضل لأننا نأخذ الحد عندما تقترب n من اللانهاية و \(\Delta x \) تصبح صغيرة بشكل لا نهائي هو مفهوم متكامل.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) يمثل المنطقة تحت f لـ x بين x = a و x = b
إيجاد التكامل هو عكس إيجاد المشتقات.
مشتق x 2 هو 2x. إذن ، تكامل 2x هو x 2 .
\(\int 2x \space dx = x^2 + C\) ، حيث C ثابت. بما أن مشتق الثابت هو 0 ، فإن مشتق x 2 ، x 2 +4 ، x 2 +10 ، x 2 +99 يساوي 2x. إذن ، تكامل 2x هو x 2 + C.
لنلقِ نظرة على تكاملات الدوال الشائعة:
| الوظائف المشتركة | دور | متكامل |
| مستمر | \(\int a \cdot dx\) | \(ax + c\) |
| عامل | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| ميدان | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| متسارع | \(\int e^x \cdot dx\) | \(e^x + c\) |
| علم المثلثات (x بالتقدير الدائري) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
قواعد التكامل المشتركة:
| قواعد | دور | متكامل |
| الضرب في ثابت | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| قاعدة الطاقة (ن <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| حكم المجموع | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| حكم الفرق | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
أصناف التكاملات
\(\int f(x) \space dx\) يمثل التكامل غير المحدد و \(\int_a^bf(x) \cdot dx\) يمثل تكاملًا محددًا. التكامل المحدد له قيم البداية والنهاية. هنا أ و ب تسمى حدود أو حدود. التكامل غير المحدد هو شكل عام للتكامل ويمكن تفسيره على أنه مضاد لاشتقاق الوظيفة.
نجد التكامل المحدد بحساب التكامل غير المحدد عند a ، وعند b ، ثم طرحه. دعونا نفهم هذا بمثال:
نحن نعلم \(\int 2x \cdot dx = x^2 + C\) . ماذا ستكون قيمة التكامل المحدد \(\int _1^2 2x \cdot dx \) ؟
عند x = 1 ، \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
عند x = 2 ، \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
اطرح (4 + C) - (1 + C) = 3
قيمة \(\int _1^2 2x \cdot dx \) = 3