Sən öyrənəcəksən:
İnteqrallar törəmələrlə birlikdə hesablamanın əsas obyektləridir. İnteqralın hesablanması prosesinə inteqrasiya , inteqralın təxmini hesablanması isə ədədi inteqrasiya adlanır.
İnteqralların iki sinfi var - müəyyən inteqral (5 kimi) və \(\int_a^bf(x) \cdot dx\) kimi aşağı və yuxarı hədləri olan qeyri-müəyyən inteqrallar.
İnteqral nədir?
Tutaq ki, əyrinin altındakı sahəni və yuxarıdakı x oxunu tapmalıyıq.
Bunun bir yolu bölgəni dörd seqmentə bölmək və sonra hər bir düzbucağın yuxarı sağ küncünün əyriyə toxunması üçün (bu seqment xəttindən istifadə edərək) bir düzbucaqlı çəkməkdir (aşağıda göstərildiyi kimi)
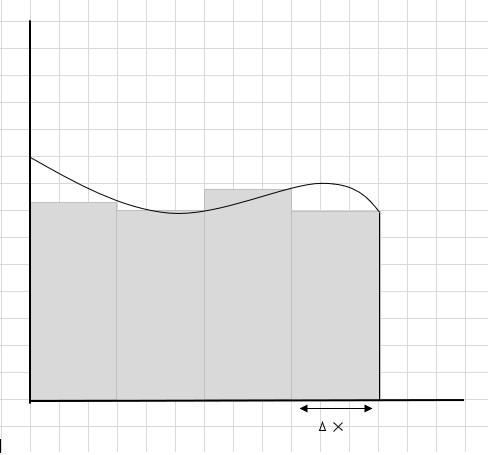
Bu düzbucaqlı seqmentlərin sahəsinin cəmi bu əyri altında təxmin edilən sahədir. \(\Delta x \) düzbucaqlıların/dilimlərin enidir. Təxmini sahə haqqında nə düşünürsünüz?
Bu əyri bölgənin sahəsi hesablanarkən bir çox əyri hissəsi buraxılır və bir neçə əlavə hissə nəzərə alınır. Şəklin altındakı qeydiyyat tünd boz bölgə buraxılmış və əlavə hissələri təmsil edir.
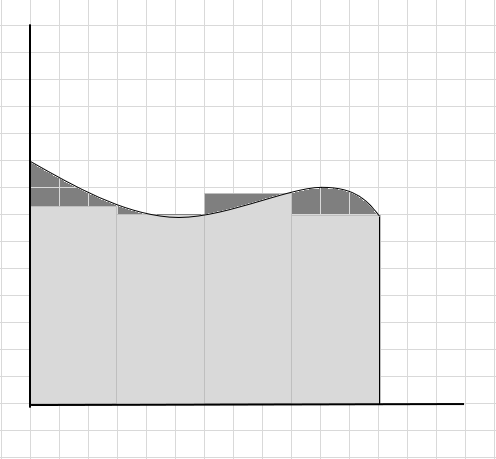
Düzbucaqlılar əyrinin altına tam uyğun gəlmədiyi üçün bunun əyri bölgənin sahəsinin zəif qiymətləndirilməsi olduğunu söyləyə bilərik. Bu əyrinin altındakı sahəni daha kiçik seqmentlərə ayıraq.
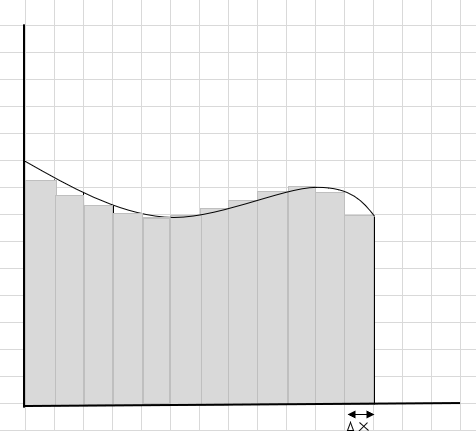
Bu düzbucaqlıların əyri sahənin içərisinə daha böyük düzbucaqlı seqmentlərdən daha yaxşı uyğunlaşdığını görə bilərsiniz. Gəlin bu əyri bölgəni daha kiçik seqmentlərə/dilimlərə bölməyə və əyrinin altındakı sahəni təyin etməyə çalışaq.
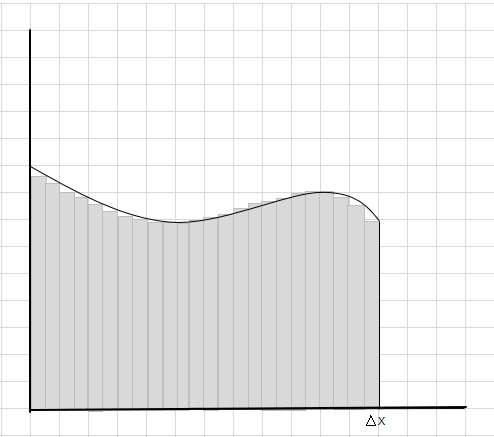
Buraxılmış və əlavə hissələr tədricən azalır və düzbucaqlılar əyri bölgənin içərisinə daha yaxşı uyğunlaşır. Belə nəticəyə gələ bilərik ki, bütün bu düzbucaqlıların sahəsinin cəmi əyri altındakı sahəni yaxşı qiymətləndirir. Və ya başqa sözlə, dilimlərin eni sıfıra yaxınlaşdıqca cavabın doğru cavaba yaxınlaşdığını söyləyə bilərik. İndi \(\Delta x\) üçün dx yazırıq ki, eni sıfıra yaxınlaşır.
Gəlin burada inteqral hesablama düsturu əldə edək:
Tutaq ki, a və b nöqtələri arasında bu əyri altındakı sahəni tapmalıyıq: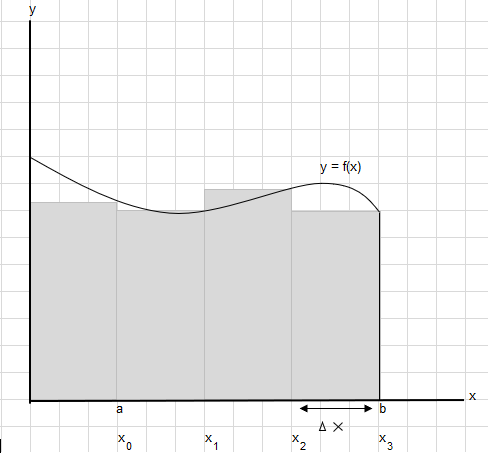
a və b arasındakı sahəni bərabər seqmentlərə bölün ki, hər düzbucağın eni \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Bu düzbucaqlıların sahəsinin cəmini \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
\(\Delta x \) kiçildikcə və ya başqa sözlə seqmentlərin sayı artdıqca biz sahənin daha yaxşı yaxınlaşmasına sahib ola bilərik. Beləliklə, \(\Delta x \) getdikcə nazikləşir və n böyüyür və böyüyür. n sonsuza yaxınlaşdıqca və \(\Delta x \) sonsuz kiçik olduqda limiti götürdükdə daha yaxşı yaxınlaşma əldə etmək anlayışı İnteqraldır.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) x = a və x = b arasında x-in f altındakı sahəni təmsil edir
İnteqralın tapılması törəmələrin tapılmasının əksidir.
x 2 -nin törəməsi 2x-dir. Beləliklə, 2x inteqralı x 2 -dir.
\(\int 2x \space dx = x^2 + C\) , burada C sabitdir. Sabitin törəməsi 0 olduğundan x 2 , x 2 +4, x 2 +10, x 2 +99 törəməsi 2x-dir. Beləliklə, 2x inteqralı x 2 +C-dir.
Ümumi funksiyaların inteqrallarına baxaq:
| Ümumi funksiyalar | Funksiya | İnteqral |
| Sabit | \(\int a \cdot dx\) | \(ax + c\) |
| Dəyişən | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Kvadrat | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Eksponensial | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Triqonometriya (x radyanla) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Ümumi İnteqrasiya Qaydaları:
| Qaydalar | Funksiya | İnteqral |
| Sabitlə vurma | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Güc Qaydası (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Toplam qaydası | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Fərq Qaydası | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
İnteqralların sinifləri
\(\int f(x) \space dx\) qeyri-müəyyən inteqralı, \(\int_a^bf(x) \cdot dx\) isə müəyyən inteqralı təmsil edir. Müəyyən bir inteqral başlanğıc və son qiymətlərə malikdir. Burada a və b hədd və ya sərhəd adlanır. Qeyri-müəyyən inteqral daha çox inteqrasiyanın ümumi formasıdır və funksiyanın anti-törəməsi kimi şərh edilə bilər.
Müəyyən İnteqralı a -da və b -də qeyri-müəyyən İnteqralı hesablayıb, sonra çıxarmaqla tapırıq. Bunu bir misalla başa düşək:
Biz bilirik \(\int 2x \cdot dx = x^2 + C\) . Müəyyən bir inteqralın qiyməti nə olacaq \(\int _1^2 2x \cdot dx \) ?
x =1-də, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2-də \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
(4 + C) - (1 + C) = 3 çıxın
\(\int _1^2 2x \cdot dx \) dəyəri = 3