তুমি শিখবে:
ডেরিভেটিভের সাথে অখণ্ডগুলি হল ক্যালকুলাসের মৌলিক বস্তু। একটি অখণ্ড গণনা করার প্রক্রিয়াটিকে একীকরণ বলা হয় এবং একটি অখণ্ডের আনুমানিক গণনাকে সংখ্যাসূচক একীকরণ বলা হয়।
অখণ্ডের দুটি শ্রেণি আছে - নির্দিষ্ট অখণ্ড (যেমন 5) এবং অনির্দিষ্ট অখণ্ড, যার নিম্ন এবং উপরের সীমা রয়েছে যেমন \(\int_a^bf(x) \cdot dx\) ।
ইন্টিগ্রাল কি?
ধরা যাক আমাদের বক্ররেখা এবং উপরের x-অক্ষের নিচের ক্ষেত্রফল খুঁজে বের করতে হবে।
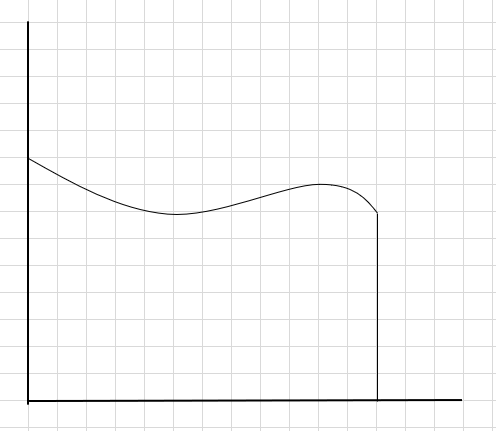
করার একটি উপায় হল অঞ্চলটিকে চারটি ভাগে ভাগ করা এবং তারপর একটি আয়তক্ষেত্র আঁকুন (এই সেগমেন্ট লাইন ব্যবহার করে) যাতে প্রতিটি আয়তক্ষেত্রের উপরের ডান কোণটি বক্ররেখাকে স্পর্শ করে (নিচে দেওয়া হয়েছে)
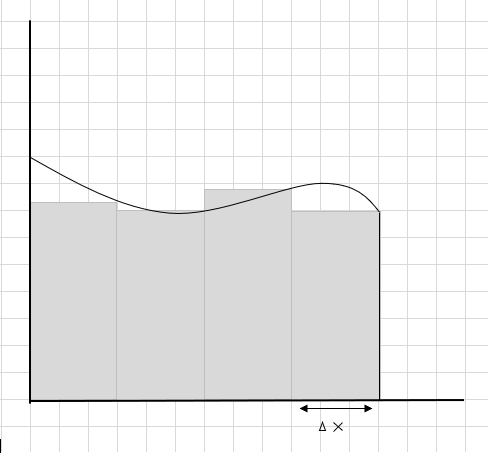
এই আয়তক্ষেত্রাকার অংশগুলির ক্ষেত্রফলের সমষ্টি হল এই বক্ররেখার আনুমানিক এলাকা। \(\Delta x \) আয়তক্ষেত্র/স্লাইসগুলির প্রস্থ। আপনি আনুমানিক এলাকা সম্পর্কে কি মনে করেন?
এই বক্র অঞ্চলের ক্ষেত্রফল গণনা করার সময় অনেকগুলি বক্র অংশ মিস করা হয় এবং কয়েকটি অতিরিক্ত অংশ বিবেচনা করা হয়। নিচের চিত্রে চেক ইন করুন গাঢ় ধূসর অঞ্চল মিস আউট এবং অতিরিক্ত অংশ প্রতিনিধিত্ব করে।
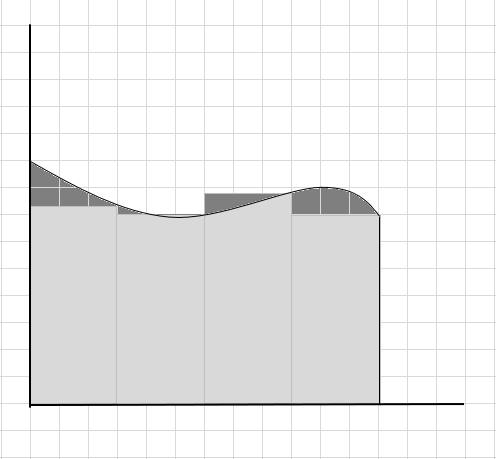
আমরা বলতে পারি এটি বাঁকা অঞ্চলের ক্ষেত্রফলের একটি দুর্বল অনুমান কারণ আয়তক্ষেত্রগুলি বক্ররেখার নীচে ঠিক ফিট করে না। এই বক্ররেখার নিচের ক্ষেত্রফলকে ছোট ছোট অংশে ভাগ করা যাক।
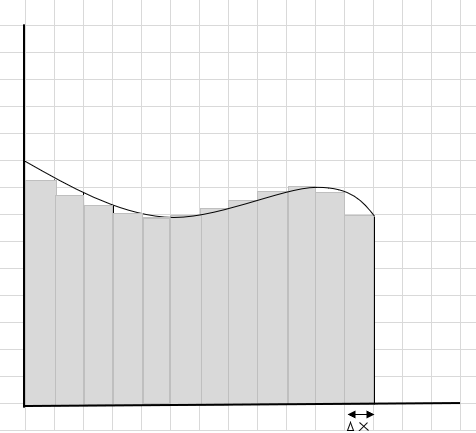
আপনি দেখতে পাচ্ছেন যে এই আয়তক্ষেত্রগুলি বৃহত্তর আয়তক্ষেত্রাকার অংশগুলির তুলনায় বাঁকা এলাকার ভিতরে ভালভাবে ফিট করে। আসুন এই বাঁকা অঞ্চলটিকে ছোট অংশে/স্লাইসে ভাগ করার চেষ্টা করি এবং বক্ররেখার নীচে ক্ষেত্রফল নির্ধারণ করার চেষ্টা করি।
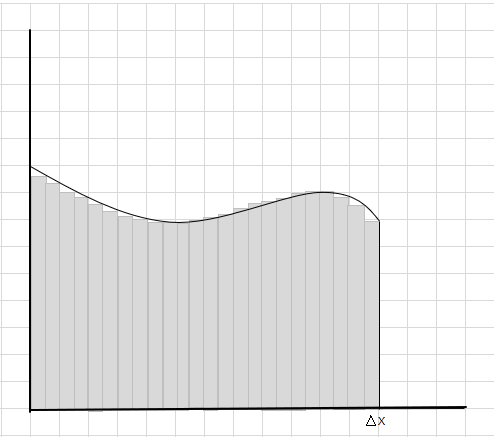
মিস এবং অতিরিক্ত অংশগুলি ধীরে ধীরে হ্রাস পাচ্ছে এবং আয়তক্ষেত্রগুলি বক্ররেখা অঞ্চলের ভিতরে অনেক ভাল ফিট করছে। আমরা অনুমান করতে পারি যে এই সমস্ত আয়তক্ষেত্রগুলির ক্ষেত্রফলের যোগফল বক্ররেখার নীচে ক্ষেত্রফলের একটি ভাল অনুমান দেয়। অথবা অন্য কথায়, আমরা বলতে পারি যে স্লাইসগুলি প্রস্থে শূন্যের কাছে আসে উত্তরটি সত্য উত্তরের কাছে আসে। আমরা এখন \(\Delta x\) জন্য dx লিখি মানে প্রস্থ শূন্যের কাছাকাছি।
চলুন এখানে ইন্টিগ্রাল ক্যালকুলাসের সূত্রটি বের করা যাক:
ধরা যাক বিন্দু a এবং b এর মধ্যে এই বক্ররেখার নিচের ক্ষেত্রফল খুঁজে বের করতে হবে: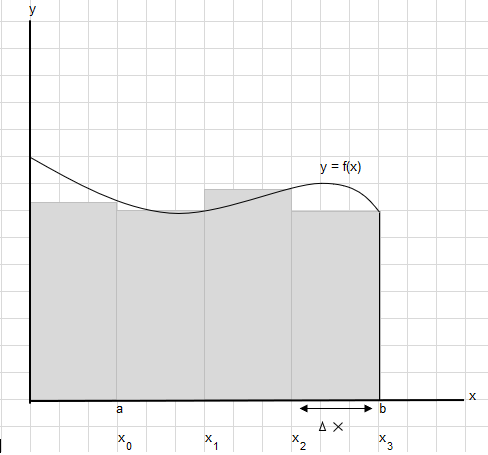
a এবং b এর ক্ষেত্রফলকে সমান ভাগে ভাগ করুন যাতে প্রতিটি আয়তক্ষেত্রের প্রস্থ হয় \(\Delta x\) ।
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
এই আয়তক্ষেত্রগুলির ক্ষেত্রফলের যোগফল \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) হিসাবে লেখা যেতে পারে।
আমরা ক্ষেত্রফলের আরও ভাল অনুমান করতে পারি কারণ \(\Delta x \) ছোট হয়ে যায় বা অন্য কথায় যখন কয়েকটি অংশ বাড়ে। সুতরাং \(\Delta x \) পাতলা থেকে পাতলা হয়ে যাচ্ছে এবং n বড় থেকে বড় হচ্ছে। n অসীমের কাছাকাছি আসার সাথে সাথে আমরা সীমাটি নিই এবং \(\Delta x \) অসীমভাবে ছোট হয়ে যাওয়ার এই ধারণাটি হল ইন্টিগ্রাল।
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) x = a এবং x = b এর মধ্যে x এর f এর নিচের ক্ষেত্রটিকে প্রতিনিধিত্ব করে
ইন্টিগ্রাল খোঁজা হল ডেরিভেটিভস খোঁজার বিপরীত।
x 2 এর ডেরিভেটিভ হল 2x। সুতরাং 2x এর একটি অখণ্ড হল x 2 ।
\(\int 2x \space dx = x^2 + C\) , যেখানে C একটি ধ্রুবক। যেহেতু ধ্রুবকের ডেরিভেটিভ 0 তাই x 2 , x 2 +4, x 2 +10, x 2 +99 এর ডেরিভেটিভ হল 2x। তাই 2x এর অখণ্ড হল x 2 +C।
আসুন সাধারণ ফাংশনগুলির অবিচ্ছেদ্যগুলি দেখি:
| সাধারণ ফাংশন | ফাংশন | অখণ্ড |
| ধ্রুবক | \(\int a \cdot dx\) | \(ax + c\) |
| পরিবর্তনশীল | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| বর্গক্ষেত্র | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| সূচকীয় | \(\int e^x \cdot dx\) | \(e^x + c\) |
| ত্রিকোণমিতি (x রেডিয়ানে) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
সাধারণ একীকরণের নিয়ম:
| নিয়ম | ফাংশন | অখণ্ড |
| ধ্রুবক দ্বারা গুণ | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| পাওয়ার নিয়ম(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| সমষ্টি নিয়ম | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| পার্থক্য নিয়ম | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
ইন্টিগ্রেলের ক্লাস
\(\int f(x) \space dx\) অনির্দিষ্ট অবিচ্ছেদ্য প্রতিনিধিত্ব করে এবং \(\int_a^bf(x) \cdot dx\) একটি নির্দিষ্ট অখণ্ডকে উপস্থাপন করে। একটি নির্দিষ্ট অবিচ্ছেদ্য শুরু এবং শেষ মান আছে। এখানে a এবং b কে সীমা বা সীমানা বলা হয়। অনির্দিষ্ট অবিচ্ছেদ্য একীকরণের একটি সাধারণ রূপ এবং ফাংশনের অ্যান্টি-ডেরিভেটিভ হিসাবে ব্যাখ্যা করা যেতে পারে।
আমরা a , এবং b তে অনির্দিষ্ট পূর্ণাঙ্গ গণনা করে, তারপর বিয়োগ করার মাধ্যমে নির্দিষ্ট অখণ্ড খুঁজে পাই। আসুন একটি উদাহরণ দিয়ে এটি বুঝতে পারি:
আমরা জানি \(\int 2x \cdot dx = x^2 + C\) । একটি নির্দিষ্ট অখণ্ডের মান কত হবে \(\int _1^2 2x \cdot dx \) ?
x =1 এ, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2 এ, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
বিয়োগ (4 + C) - (1 + C) = 3
এর মান \(\int _1^2 2x \cdot dx \) = 3