Du wirst es lernen:
Integrale zusammen mit Ableitungen sind die grundlegenden Objekte in der Analysis. Der Prozess der Berechnung eines Integrals wird als Integration bezeichnet, und die ungefähre Berechnung eines Integrals wird als numerische Integration bezeichnet.
Es gibt zwei Klassen von Integralen - bestimmte Integrale (wie 5) und unbestimmte Integrale, die untere und obere Grenzen haben wie \(\int_a^bf(x) \cdot dx\) .
Was ist integral?
Nehmen wir an, wir müssen die Fläche unter der Kurve und der darüber liegenden x-Achse finden.
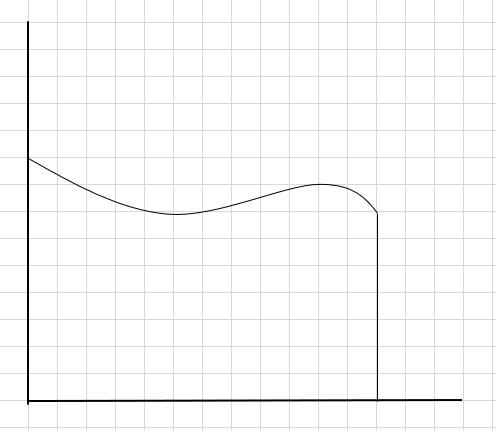
Eine Möglichkeit besteht darin, die Region in vier Segmente zu unterteilen und dann ein Rechteck (unter Verwendung dieser Segmentlinie) so zu zeichnen, dass die obere rechte Ecke jedes Rechtecks die Kurve berührt (wie unten angegeben).
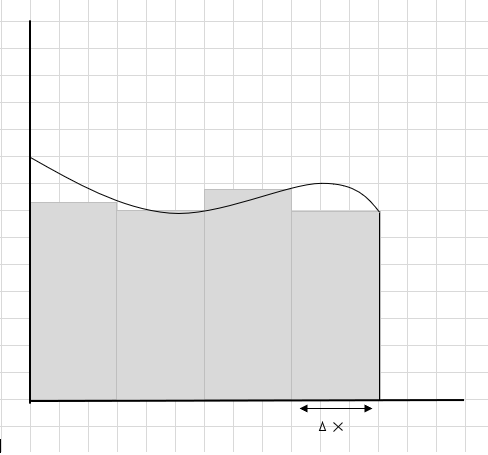
Die Summe der Fläche dieser rechteckigen Segmente ist die geschätzte Fläche unter dieser Kurve. \(\Delta x \) ist die Breite der Rechtecke/Slices. Was haltet ihr von der geschätzten Fläche?
Bei der Berechnung der Fläche dieses Kurvenbereichs werden viele Kurventeile übersehen und einige zusätzliche Teile berücksichtigt. Check-in unter dem dunkelgrauen Bereich des Bildes stellt fehlende und zusätzliche Teile dar.
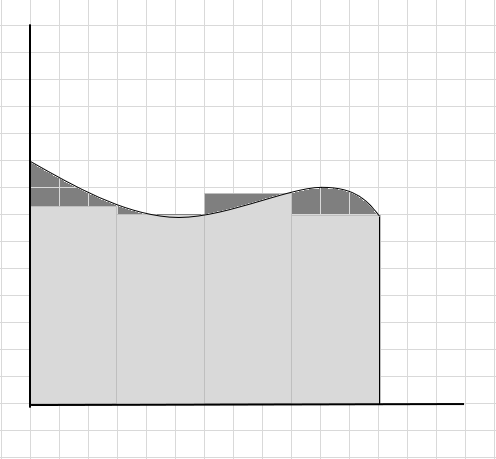
Wir können sagen, dass dies eine schlechte Schätzung der Fläche des gekrümmten Bereichs ist, da Rechtecke nicht genau unter die Kurve passen. Lassen Sie uns die Fläche unter dieser Kurve in kleinere Segmente unterteilen.
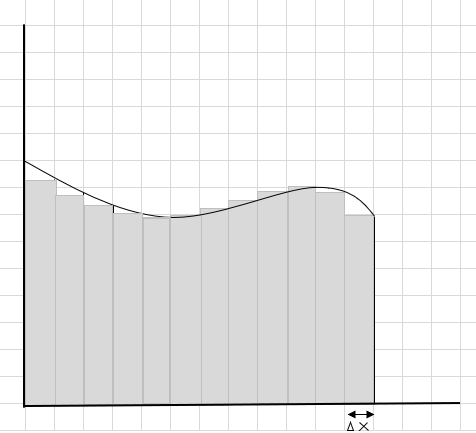
Sie können sehen, dass diese Rechtecke besser in den gekrümmten Bereich passen als die größeren rechteckigen Segmente. Lassen Sie uns versuchen, diesen gekrümmten Bereich in kleinere Segmente/Scheiben zu unterteilen und versuchen, die Fläche unter der Kurve zu bestimmen.
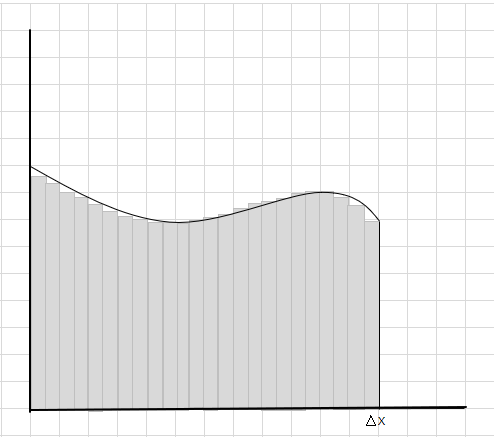
Die fehlenden und zusätzlichen Teile werden allmählich reduziert und Rechtecke passen viel besser in den Kurvenbereich. Wir können daraus schließen, dass die Summe der Flächen aller dieser Rechtecke eine gute Schätzung der Fläche unter der Kurve ergibt. Oder mit anderen Worten, wir können sagen, dass sich die Antwort der wahren Antwort nähert, wenn sich die Slices in der Breite Null nähern. Wir schreiben jetzt dx für \(\Delta x\) um zu bedeuten, dass die Breite gegen Null geht.
Lassen Sie uns hier die Formel für die Integralrechnung herleiten:
Nehmen wir an, wir müssen die Fläche unter dieser Kurve zwischen Punkt a und b finden: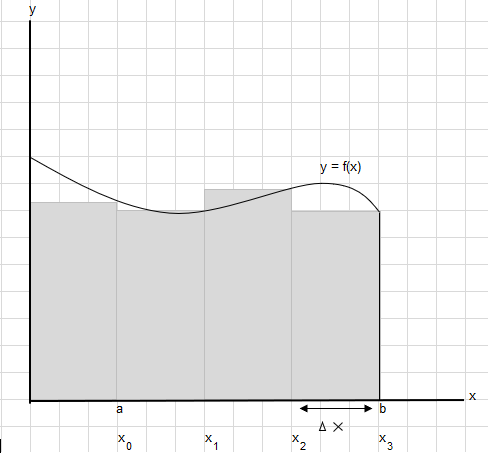
Teilen Sie die Fläche zwischen a und b in gleiche Segmente, so dass die Breite jedes Rechtecks \(\Delta x\) ist.
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Die Summe der Flächen dieser Rechtecke kann geschrieben werden als \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Wir können eine bessere Approximation der Fläche haben, wenn \(\Delta x \) kleiner wird, oder mit anderen Worten, wenn die Anzahl der Segmente zunimmt. Also wird \(\Delta x \) immer dünner und n immer größer. Diese Vorstellung, eine bessere Annäherung zu erhalten, wenn wir die Grenze nehmen, wenn n gegen unendlich geht und \(\Delta x \) infinitesimal klein wird, ist integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) repräsentiert die Fläche unter f von x zwischen x = a und x = b
Das Finden von Integralen ist eine Umkehrung des Findens von Ableitungen.
Ableitung von x 2 ist 2x. Ein Integral von 2x ist also x 2 .
\(\int 2x \space dx = x^2 + C\) , wobei C eine Konstante ist. Da die Ableitung der Konstante 0 ist, ist die Ableitung von x 2 , x 2 +4, x 2 +10, x 2 +99 2x. Daher ist das Integral von 2x x 2 +C.
Betrachten wir Integrale gemeinsamer Funktionen:
| Gemeinsame Funktionen | Funktion | Integral |
| Konstante | \(\int a \cdot dx\) | \(ax + c\) |
| Variable | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Quadrat | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Exponentiell | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometrie (x im Bogenmaß) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Gemeinsame Integrationsregeln:
| Regeln | Funktion | Integral |
| Multiplikation mit Konstante | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Potenzregel(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Summenregel | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Differenzregel | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Klassen von Integralen
\(\int f(x) \space dx\) repräsentiert das unbestimmte Integral und \(\int_a^bf(x) \cdot dx\) repräsentiert ein bestimmtes Integral. Ein bestimmtes Integral hat Anfangs- und Endwerte. Hier werden a und b Grenzen oder Begrenzungen genannt. Das unbestimmte Integral ist eher eine allgemeine Form der Integration und kann als Stammfunktion der Funktion interpretiert werden.
Wir finden das bestimmte Integral, indem wir das unbestimmte Integral bei a und bei b berechnen und dann subtrahieren. Lassen Sie uns dies an einem Beispiel verstehen:
Wir kennen \(\int 2x \cdot dx = x^2 + C\) . Welchen Wert hat ein bestimmtes Integral \(\int _1^2 2x \cdot dx \) ?
Bei x = 1 \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Bei x = 2 \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Subtrahiere (4 + C) - (1 + C) = 3
Wert von \(\int _1^2 2x \cdot dx \) = 3