You will learn:
Integrals together with derivatives are the fundamental objects in calculus. The process of computing an integral is called integration and approximate computation of an integral is termed as numerical integration.
There are two classes of integrals - definite integral (like 5) and Indefinite integrals, which has lower and upper limits like \(\int_a^b f(x) \cdot dx\).
What is Integral?
Let say we have to find the area under the curve and the above x-axis.
One way to do is to divide the region into four segments and then draw a rectangle(using this segment line) such that the upper right corner of each rectangle touches the curve(as given below)
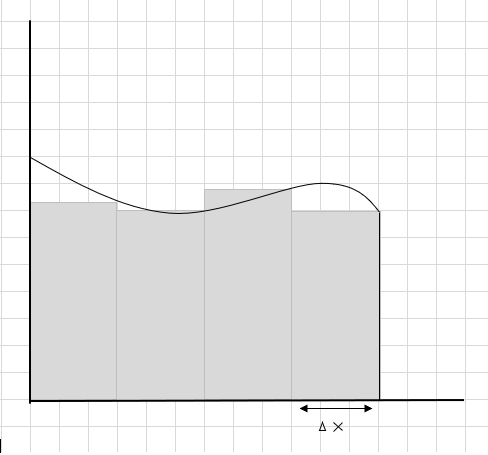
The sum of the area of these rectangular segments is the estimated area under this curve. \(\Delta x \) being the width of the rectangles/slices. What do you think about the estimated area?
A lot of curve part is missed and a few additional parts is considered while calculating the area of this curve region. Check-in below image dark gray region represents miss out and additional parts.
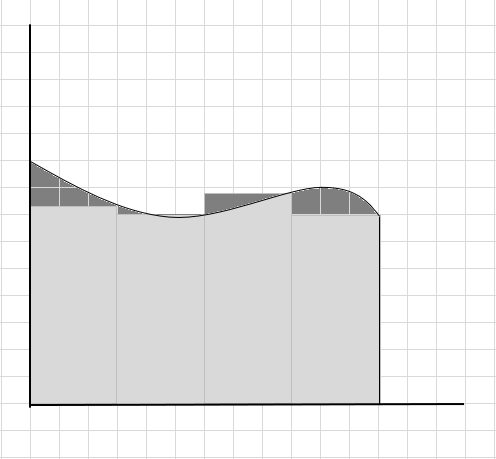
We can say this is a poor estimation of the area of the curved region as rectangles do not exactly fit under the curve. Let's divide the area under this curve into smaller segments.
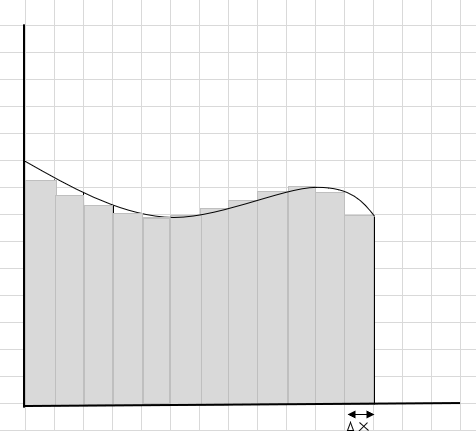
You can see that these rectangles fit inside the curved area better than the larger rectangular segments. Let's try dividing this curved region into smaller segments/slices and try to determine the area under the curve.
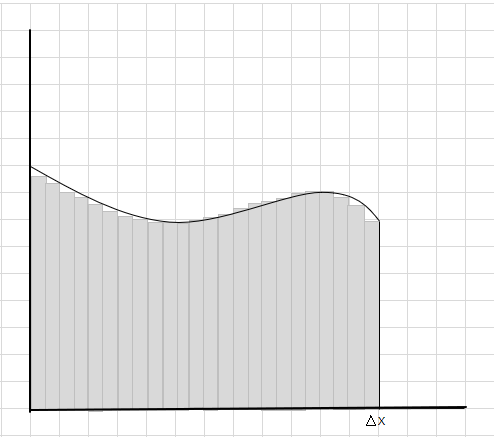
The miss and extra parts are gradually reducing and rectangles are fitting much better inside the curve region. We can infer that sum of the area of all these rectangles gives a good estimate of the area under the curve. Or in other words, we can say as the slices approach zero in width the answer approaches the true answer. We now write dx for \(\Delta x\) to means that the width is approaching zero.
Let's derive the formula for integral calculus here:
Let say we need to find the area under this curve between point a and b:
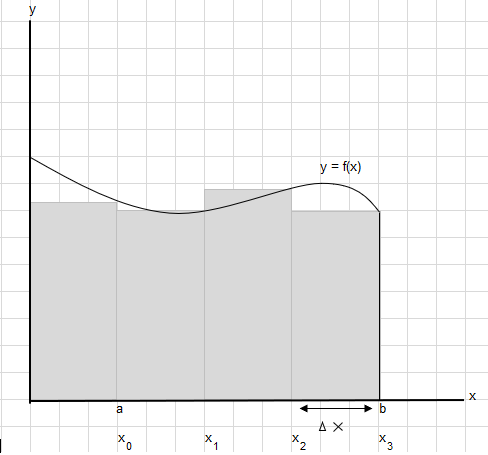
Divide the area between a and b into equal segments such that the width of each rectangle is \(\Delta x\).
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
The sum of area of these rectangles can be written as \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\).
We can have a better approximation of area as \(\Delta x \) gets smaller or in other words when a number of segments increases. So \(\Delta x \) gets thinner and thinner and n gets larger and larger. This notion of getting better approximation as we take the limit as n approaches infinity and \(\Delta x \) becoming infinitesimally small is Integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^b f(x) \space dx\)
\(\int_a^b f(x) \space dx\) represents the area under f of x between x = a and x = b
Finding Integral is a reverse of finding Derivatives.
Derivative of x2 is 2x. So an integral of 2x is x2.
\(\int 2x \space dx = x^2 + C\), where C is a constant. As derivative of constant is 0 hence derivative of x2, x2+4, x2+10, x2+99 is 2x. Therefore integral of 2x is x2+C.
Let's look at integrals of common functions:
| Common Functions | Function | Integral |
| Constant | \(\int a \cdot dx\) | \(ax + c\) |
| Variable | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Square | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Exponential | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometry(x in radians) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Common Integration Rules:
| Rules | Function | Integral |
| Multiplication by constant | \(\int c f(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Power Rule(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Sum Rule | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Difference Rule | \(\int (f-g)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Classes of Integrals
\(\int f(x) \space dx\) represent the indefinite integral and \(\int_a^b f(x) \cdot dx\) represents a definite integral. A definite integral has start and end values. Here a and b is called limits or boundaries. The indefinite integral is more of a general form of integration and can be interpreted as anti-derivative of the function.
We find the Definite Integral by calculating the indefinite Integral at a, and at b, then subtracting. Let us understand this by an example:
We know \(\int 2x \cdot dx = x^2 + C\). What will be the value of a definite integral \(\int _1^2 2x \cdot dx \) ?
At x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
At x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Subtract (4 + C) - (1 + C) = 3
Value of \(\int _1^2 2x \cdot dx \) = 3