Aprenderás:
Las integrales junto con las derivadas son los objetos fundamentales del cálculo. El proceso de cálculo de una integral se denomina integración y el cálculo aproximado de una integral se denomina integración numérica.
Hay dos clases de integrales: la integral definida (como 5) y la integral indefinida, que tiene límites inferior y superior como \(\int_a^bf(x) \cdot dx\) .
¿Qué es Integral?
Digamos que tenemos que encontrar el área bajo la curva y el eje x de arriba.
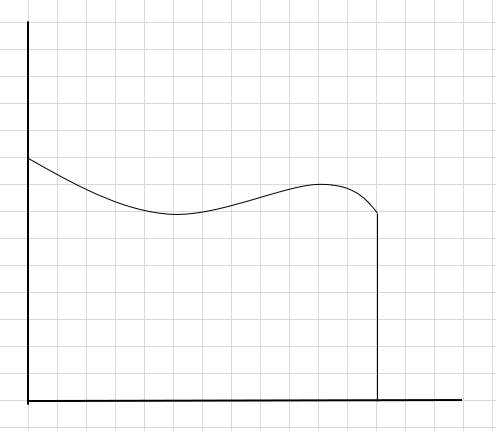
Una forma de hacerlo es dividir la región en cuatro segmentos y luego dibujar un rectángulo (usando esta línea de segmento) de modo que la esquina superior derecha de cada rectángulo toque la curva (como se indica a continuación)
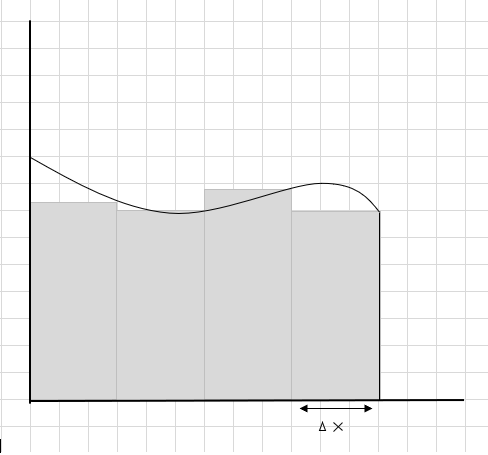
La suma del área de estos segmentos rectangulares es el área estimada bajo esta curva. \(\Delta x \) siendo el ancho de los rectángulos/rebanadas. ¿Qué opinas sobre el área estimada?
Se pierde una gran parte de la curva y se consideran algunas partes adicionales al calcular el área de esta región de la curva. El check-in debajo de la región gris oscuro de la imagen representa piezas perdidas y adicionales.
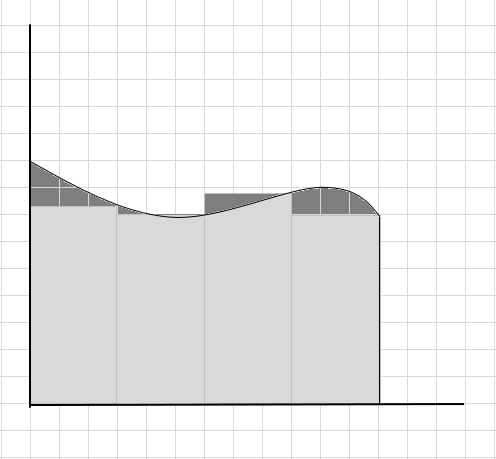
Podemos decir que esta es una mala estimación del área de la región curva ya que los rectángulos no encajan exactamente debajo de la curva. Dividamos el área bajo esta curva en segmentos más pequeños.
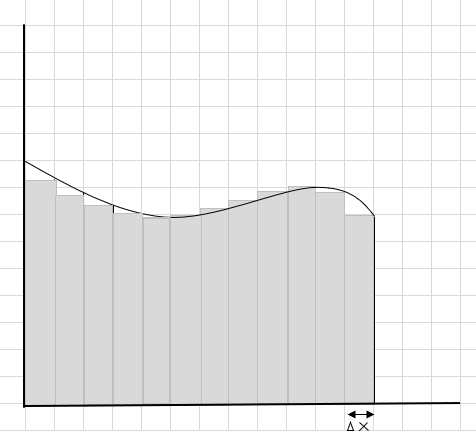
Puedes ver que estos rectángulos encajan mejor dentro del área curva que los segmentos rectangulares más grandes. Intentemos dividir esta región curva en segmentos/cortes más pequeños e intentemos determinar el área bajo la curva.
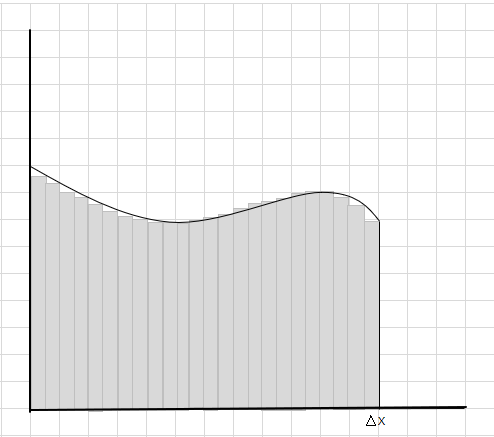
Las partes faltantes y adicionales se reducen gradualmente y los rectángulos se ajustan mucho mejor dentro de la región de la curva. Podemos inferir que la suma del área de todos estos rectángulos da una buena estimación del área bajo la curva. O, en otras palabras, podemos decir que a medida que los cortes se acercan a cero en ancho, la respuesta se acerca a la respuesta verdadera. Ahora escribimos dx para \(\Delta x\) para que signifique que el ancho se aproxima a cero.
Derivamos la fórmula para el cálculo integral aquí:
Digamos que necesitamos encontrar el área bajo esta curva entre los puntos a y b: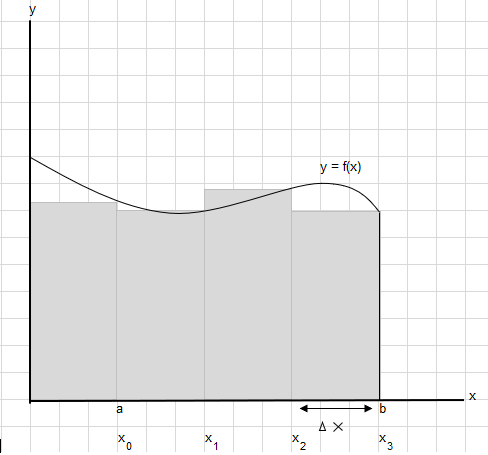
Divide el área entre a y b en segmentos iguales de modo que el ancho de cada rectángulo sea \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
La suma del área de estos rectángulos se puede escribir como \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Podemos tener una mejor aproximación del área a medida que \(\Delta x \) se hace más pequeño o, en otras palabras, cuando aumenta el número de segmentos. Entonces \(\Delta x \) se vuelve más y más delgada y n se vuelve más y más grande. Esta noción de obtener una mejor aproximación a medida que tomamos el límite cuando n se acerca al infinito y \(\Delta x \) se vuelve infinitesimalmente pequeño es Integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) representa el área bajo f de x entre x = a y x = b
Encontrar integrales es lo contrario de encontrar derivadas.
La derivada de x 2 es 2x. Entonces una integral de 2x es x 2 .
\(\int 2x \space dx = x^2 + C\) , donde C es una constante. Como la derivada de la constante es 0, la derivada de x 2 , x 2 +4, x 2 +10, x 2 +99 es 2x. Por lo tanto integral de 2x es x 2 +C.
Veamos integrales de funciones comunes:
| Funciones comunes | Función | Integral |
| Constante | \(\int a \cdot dx\) | \(ax + c\) |
| Variable | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Cuadrado | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Exponencial | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometría(x en radianes) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Reglas comunes de integración:
| Normas | Función | Integral |
| Multiplicación por constante | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Regla de potencia (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| regla de la suma | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Regla de diferencia | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
clases de integrales
\(\int f(x) \space dx\) representa la integral indefinida y \(\int_a^bf(x) \cdot dx\) representa una integral definida. Una integral definida tiene valores iniciales y finales. Aquí a y b se llaman límites o fronteras. La integral indefinida es más una forma general de integración y puede interpretarse como antiderivada de la función.
Encontramos la integral definida calculando la integral indefinida en a y en b y luego restando. Entendamos esto con un ejemplo:
Sabemos \(\int 2x \cdot dx = x^2 + C\) . ¿Cuál será el valor de una integral definida \(\int _1^2 2x \cdot dx \) ?
En x = 1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
En x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Restar (4 + C) - (1 + C) = 3
Valor de \(\int _1^2 2x \cdot dx \) = 3