یاد خواهید گرفت:
انتگرال ها همراه با مشتقات اشیای اساسی در حساب دیفرانسیل و انتگرال هستند. فرآیند محاسبه یک انتگرال را یکپارچه سازی و محاسبه تقریبی یک انتگرال را انتگرال عددی می نامند.
دو دسته از انتگرال ها وجود دارد - انتگرال معین (مانند 5) و انتگرال نامعین که دارای محدودیت های پایین و بالایی مانند \(\int_a^bf(x) \cdot dx\) .
انتگرال چیست؟
فرض کنید باید ناحیه زیر منحنی و محور x بالا را پیدا کنیم.
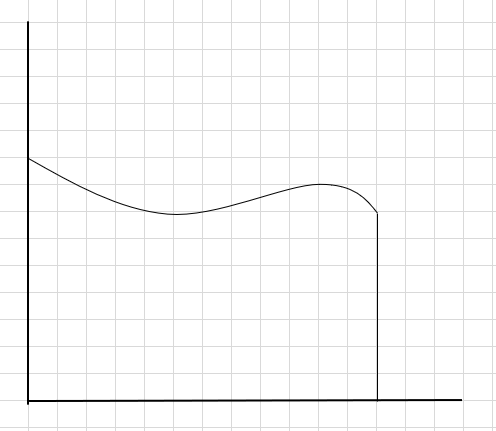
یکی از راههای انجام این کار این است که منطقه را به چهار بخش تقسیم کنید و سپس یک مستطیل بکشید (با استفاده از این خط قطعه) به طوری که گوشه سمت راست بالای هر مستطیل منحنی را لمس کند (مانند زیر).
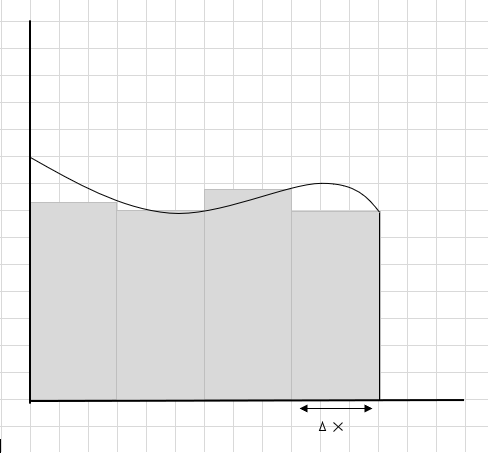
مجموع مساحت این قطعات مستطیلی، مساحت تخمین زده شده زیر این منحنی است. \(\Delta x \) عرض مستطیل ها/برش ها است. نظر شما در مورد مساحت تخمینی چیست؟
هنگام محاسبه مساحت این ناحیه منحنی، قسمت زیادی از منحنی از قلم افتاده و چند قسمت اضافی در نظر گرفته می شود. اعلام حضور در تصویر زیر منطقه خاکستری تیره نشاندهنده بخشهای از دست رفته و اضافی است.
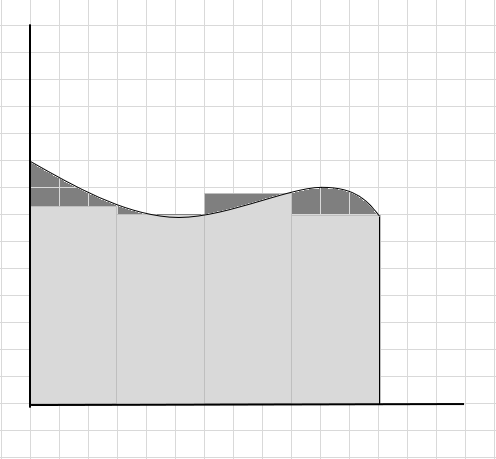
می توان گفت که این تخمین ضعیفی از مساحت ناحیه منحنی است زیرا مستطیل ها دقیقاً زیر منحنی قرار نمی گیرند. بیایید منطقه زیر این منحنی را به بخش های کوچکتر تقسیم کنیم.
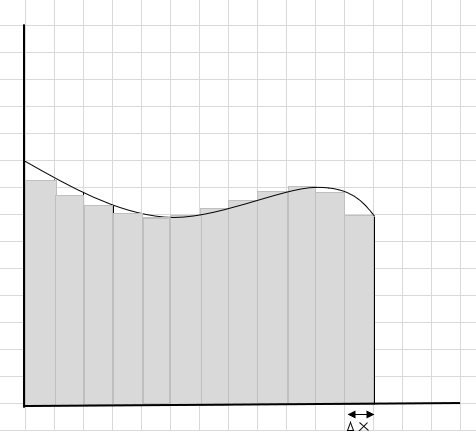
می بینید که این مستطیل ها در داخل ناحیه منحنی بهتر از بخش های مستطیلی بزرگتر قرار می گیرند. بیایید سعی کنیم این ناحیه منحنی را به بخش ها/برش های کوچکتر تقسیم کنیم و سعی کنیم ناحیه زیر منحنی را تعیین کنیم.
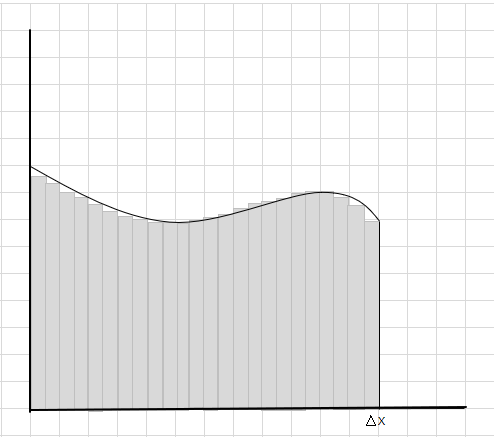
فقدان و قسمت های اضافی به تدریج کاهش می یابد و مستطیل ها بسیار بهتر در داخل منطقه منحنی قرار می گیرند. می توان نتیجه گرفت که مجموع مساحت همه این مستطیل ها تخمین خوبی از مساحت زیر منحنی می دهد. یا به عبارت دیگر، میتوان گفت با نزدیک شدن عرض برشها به صفر، پاسخ به پاسخ واقعی نزدیک میشود. اکنون dx را برای \(\Delta x\) می نویسیم تا به این معنی باشد که عرض به صفر نزدیک می شود.
بیایید فرمول حساب انتگرال را در اینجا استخراج کنیم:
فرض کنید باید مساحت زیر این منحنی را بین نقطه a و b پیدا کنیم: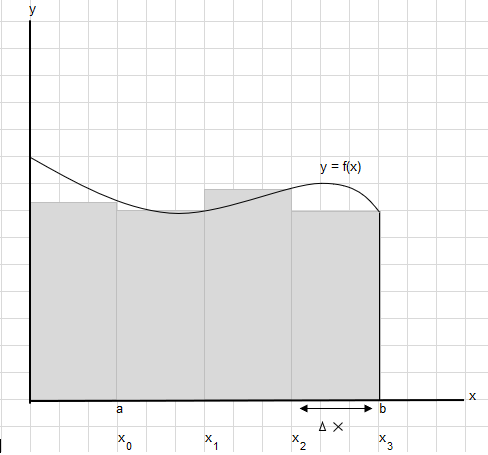
مساحت بین a و b را به قطعات مساوی تقسیم کنید به طوری که عرض هر مستطیل \(\Delta x\) باشد.
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
مجموع مساحت این مستطیل ها را می توان به صورت \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) نوشت.
وقتی \(\Delta x \) کوچکتر می شود یا به عبارت دیگر وقتی تعدادی از بخش ها افزایش می یابد، می توانیم تقریب بهتری از مساحت داشته باشیم. بنابراین \(\Delta x \) نازکتر و نازکتر میشود و n بزرگتر و بزرگتر میشود. این تصور از تقریب بهتر با نزدیک شدن n به بی نهایت و کوچک شدن \(\Delta x \) انتگرال است.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) نشان دهنده مساحت زیر f از x بین x = a و x = b است.
یافتن انتگرال معکوس یافتن مشتقات است.
مشتق x 2 2x است. بنابراین انتگرال 2x برابر با 2 است.
\(\int 2x \space dx = x^2 + C\) که C یک ثابت است. از آنجایی که مشتق ثابت 0 است، بنابراین مشتق x 2 ، x 2 +4، x 2 +10، x 2 +99 2x است. بنابراین انتگرال 2x x 2 +C است.
بیایید به انتگرال توابع رایج نگاه کنیم:
| توابع مشترک | تابع | انتگرال |
| ثابت | \(\int a \cdot dx\) | \(ax + c\) |
| متغیر | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| مربع | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| نمایی | \(\int e^x \cdot dx\) | \(e^x + c\) |
| مثلثات (x بر حسب رادیان) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
قوانین یکپارچه سازی مشترک:
| قوانین | تابع | انتگرال |
| ضرب در ثابت | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| قانون قدرت (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| قانون جمع | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| قانون تفاوت | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
کلاس های انتگرال
\(\int f(x) \space dx\) نشان دهنده انتگرال نامعین و \(\int_a^bf(x) \cdot dx\) یک انتگرال معین را نشان می دهد. یک انتگرال معین دارای مقادیر شروع و پایان است. در اینجا a و b حد یا مرز نامیده می شود. انتگرال نامعین بیشتر یک شکل کلی از ادغام است و می تواند به عنوان ضد مشتق تابع تفسیر شود.
انتگرال معین را با محاسبه انتگرال نامعین در a و در b و سپس تفریق مییابیم. اجازه دهید این را با یک مثال درک کنیم:
ما می دانیم \(\int 2x \cdot dx = x^2 + C\) . مقدار یک انتگرال معین \(\int _1^2 2x \cdot dx \) چقدر خواهد بود؟
در x =1، \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
در x = 2، \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
تفریق (4 + C) - (1 + C) = 3
مقدار \(\int _1^2 2x \cdot dx \) = 3