Tu vas apprendre:
Les intégrales et les dérivées sont les objets fondamentaux du calcul. Le processus de calcul d'une intégrale est appelé intégration et le calcul approximatif d'une intégrale est appelé intégration numérique.
Il existe deux classes d'intégrales - les intégrales définies (comme 5) et les intégrales indéfinies, qui ont des limites inférieures et supérieures telles que \(\int_a^bf(x) \cdot dx\) .
C'est quoi Intégrale ?
Disons que nous devons trouver l'aire sous la courbe et l'axe des x ci-dessus.
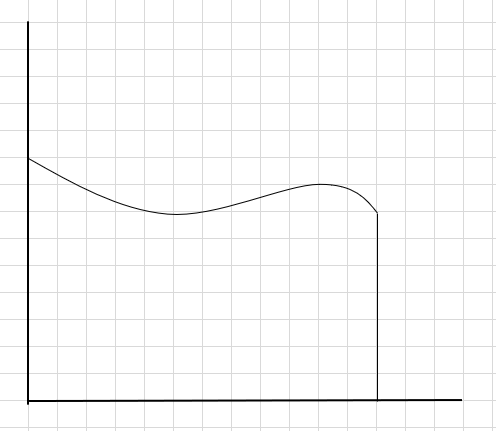
Une façon de faire est de diviser la région en quatre segments, puis de dessiner un rectangle (en utilisant cette ligne de segment) de sorte que le coin supérieur droit de chaque rectangle touche la courbe (comme indiqué ci-dessous)
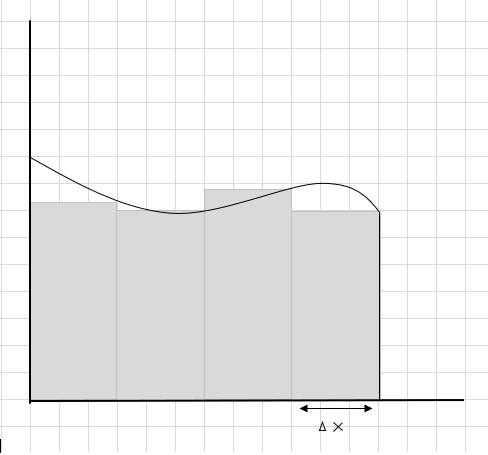
La somme de l'aire de ces segments rectangulaires est l'aire estimée sous cette courbe. \(\Delta x \) étant la largeur des rectangles/tranches. Que pensez-vous de la surface estimée ?
Une grande partie de la courbe est manquée et quelques parties supplémentaires sont prises en compte lors du calcul de l'aire de cette région de courbe. L'enregistrement sous l'image en gris foncé représente les pièces manquantes et supplémentaires.
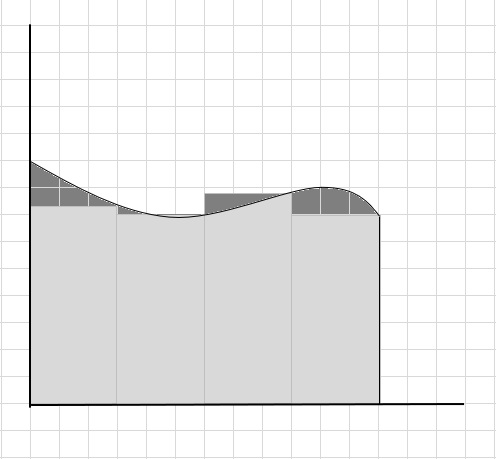
Nous pouvons dire qu'il s'agit d'une mauvaise estimation de l'aire de la région courbe car les rectangles ne rentrent pas exactement sous la courbe. Divisons la zone sous cette courbe en segments plus petits.
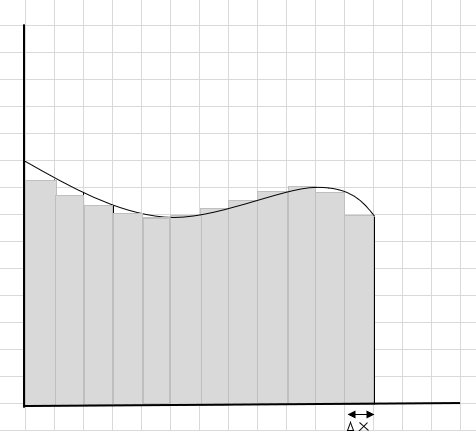
Vous pouvez voir que ces rectangles s'intègrent mieux à l'intérieur de la zone courbe que les segments rectangulaires plus grands. Essayons de diviser cette région courbe en segments/tranches plus petits et essayons de déterminer la zone sous la courbe.
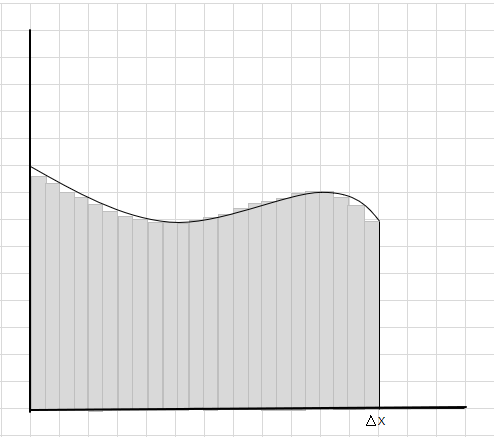
Les pièces manquantes et supplémentaires diminuent progressivement et les rectangles s'adaptent beaucoup mieux à l'intérieur de la région de la courbe. Nous pouvons en déduire que la somme de l'aire de tous ces rectangles donne une bonne estimation de l'aire sous la courbe. Ou en d'autres termes, nous pouvons dire que lorsque les tranches approchent de zéro en largeur, la réponse se rapproche de la vraie réponse. Nous écrivons maintenant dx pour \(\Delta x\) pour signifier que la largeur approche de zéro.
Dérivons ici la formule du calcul intégral :
Disons que nous devons trouver l'aire sous cette courbe entre les points a et b :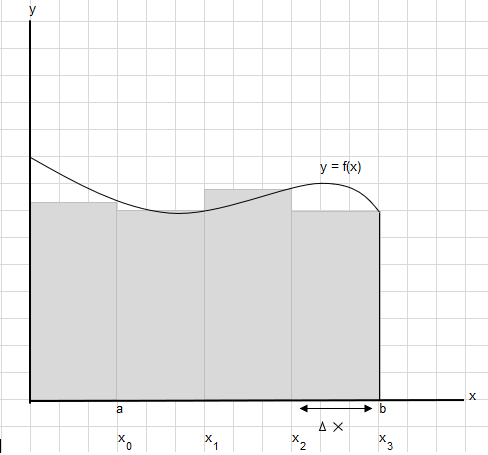
Divisez la zone entre a et b en segments égaux de sorte que la largeur de chaque rectangle soit \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
La somme des aires de ces rectangles peut être écrite comme \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Nous pouvons avoir une meilleure approximation de l'aire lorsque \(\Delta x \) devient plus petit ou, en d'autres termes, lorsque le nombre de segments augmente. Donc \(\Delta x \) devient de plus en plus mince et n devient de plus en plus grand. Cette notion d'obtenir une meilleure approximation lorsque nous prenons la limite lorsque n s'approche de l'infini et que \(\Delta x \) devient infiniment petit est intégrale.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) représente l'aire sous f de x entre x = a et x = b
Trouver l'intégrale est l'inverse de la recherche des dérivées.
La dérivée de x 2 est 2x. Donc une intégrale de 2x est x 2 .
\(\int 2x \space dx = x^2 + C\) , où C est une constante. Comme la dérivée de la constante est 0, la dérivée de x 2 , x 2 +4, x 2 +10, x 2 +99 est 2x. Donc l'intégrale de 2x est x 2 +C.
Regardons les intégrales des fonctions communes :
| Fonctions communes | Fonction | Intégral |
| Constant | \(\int a \cdot dx\) | \(ax + c\) |
| Variable | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Carré | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Exponentiel | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonométrie(x en radians) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Règles d'intégration communes :
| Règles | Fonction | Intégral |
| Multiplication par constante | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Règle de puissance(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Règle de somme | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Règle de différence | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Classes d'intégrales
\(\int f(x) \space dx\) représente l'intégrale indéfinie et \(\int_a^bf(x) \cdot dx\) représente une intégrale définie. Une intégrale définie a des valeurs de début et de fin. Ici, a et b sont appelés limites ou frontières. L'intégrale indéfinie est plus une forme générale d'intégration et peut être interprétée comme anti-dérivée de la fonction.
Nous trouvons l'intégrale définie en calculant l'intégrale indéfinie en a , et en b , puis en soustrayant. Comprenons cela par un exemple :
Nous savons \(\int 2x \cdot dx = x^2 + C\) . Quelle sera la valeur d'une intégrale définie \(\int _1^2 2x \cdot dx \) ?
A x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
À x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Soustraire (4 + C) - (1 + C) = 3
Valeur de \(\int _1^2 2x \cdot dx \) = 3