आपको सीखना होगा:
डेरिवेटिव के साथ इंटीग्रल कैलकुलस में मूलभूत वस्तुएं हैं। इंटीग्रल की गणना की प्रक्रिया को इंटीग्रेशन कहा जाता है और इंटीग्रल की अनुमानित गणना को न्यूमेरिकल इंटीग्रेशन कहा जाता है।
इंटीग्रल के दो वर्ग हैं - निश्चित इंटीग्रल (जैसे 5) और अनिश्चित इंटीग्रल, जिनकी निचली और ऊपरी सीमाएं हैं जैसे \(\int_a^bf(x) \cdot dx\) ।
इंटीग्रल क्या है?
मान लीजिए कि हमें वक्र और उपरोक्त x-अक्ष के नीचे का क्षेत्रफल ज्ञात करना है।
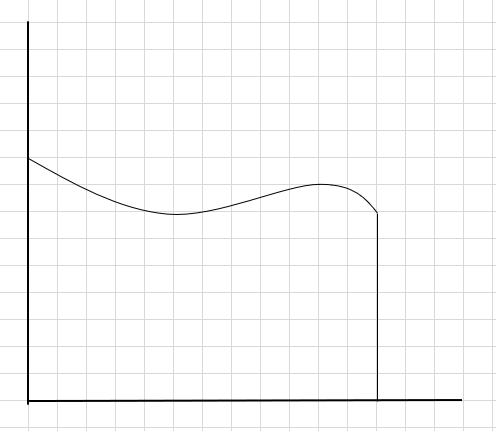
ऐसा करने का एक तरीका यह है कि क्षेत्र को चार खंडों में विभाजित किया जाए और फिर एक आयत (इस खंड रेखा का उपयोग करके) को इस तरह से खींचा जाए कि प्रत्येक आयत का ऊपरी दायां कोना वक्र को स्पर्श करे (जैसा कि नीचे दिया गया है)
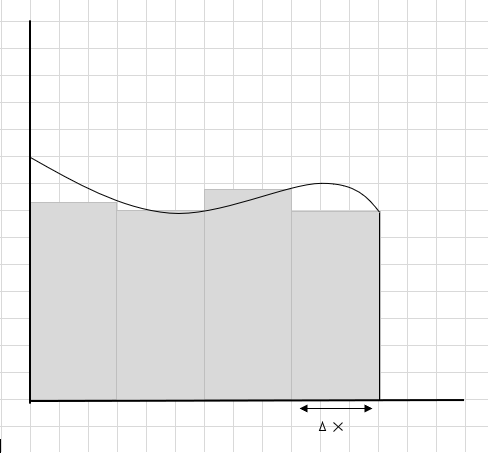
इन आयताकार खंडों के क्षेत्रफल का योग इस वक्र के अंतर्गत अनुमानित क्षेत्रफल है। \(\Delta x \) आयतों/स्लाइसों की चौड़ाई होने के कारण। अनुमानित क्षेत्रफल के बारे में आप क्या सोचते हैं?
इस वक्र क्षेत्र के क्षेत्रफल की गणना करते समय बहुत से वक्र भाग छूट जाते हैं और कुछ अतिरिक्त भागों पर विचार किया जाता है। नीचे दी गई छवि में चेक-इन गहरे भूरे रंग का क्षेत्र मिस आउट और अतिरिक्त भागों का प्रतिनिधित्व करता है।
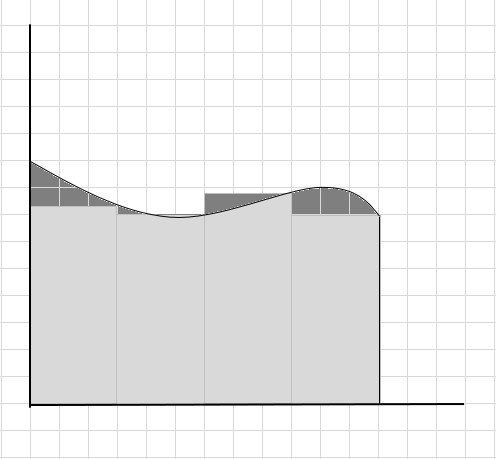
हम कह सकते हैं कि यह घुमावदार क्षेत्र के क्षेत्रफल का एक खराब अनुमान है क्योंकि आयताकार वक्र के नीचे बिल्कुल फिट नहीं होते हैं। आइए इस वक्र के नीचे के क्षेत्र को छोटे खंडों में विभाजित करें।
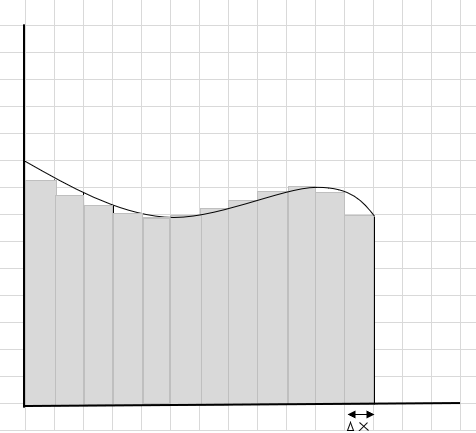
आप देख सकते हैं कि ये आयत बड़े आयताकार खंडों की तुलना में घुमावदार क्षेत्र के अंदर बेहतर फिट होते हैं। आइए इस घुमावदार क्षेत्र को छोटे खंडों/स्लाइसों में विभाजित करने का प्रयास करें और वक्र के नीचे के क्षेत्र को निर्धारित करने का प्रयास करें।
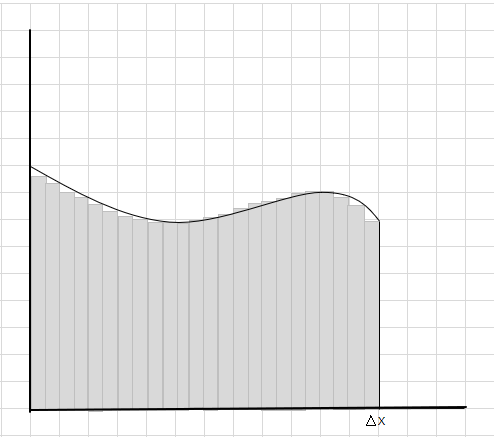
मिस और अतिरिक्त हिस्से धीरे-धीरे कम हो रहे हैं और वक्र क्षेत्र के अंदर आयत बहुत बेहतर तरीके से फिट हो रहे हैं। हम अनुमान लगा सकते हैं कि इन सभी आयतों के क्षेत्रफल का योग वक्र के नीचे के क्षेत्रफल का एक अच्छा अनुमान देता है। या दूसरे शब्दों में, हम कह सकते हैं कि जैसे-जैसे स्लाइस चौड़ाई में शून्य के करीब पहुंचते हैं, उत्तर सही उत्तर के करीब पहुंचता है। अब हम \(\Delta x\) के लिए dx लिखते हैं, जिसका अर्थ है कि चौड़ाई शून्य के करीब पहुंच रही है।
आइए यहाँ समाकलन के लिए सूत्र प्राप्त करें:
मान लीजिए कि हमें इस वक्र के नीचे बिंदु a और b के बीच का क्षेत्र खोजने की आवश्यकता है: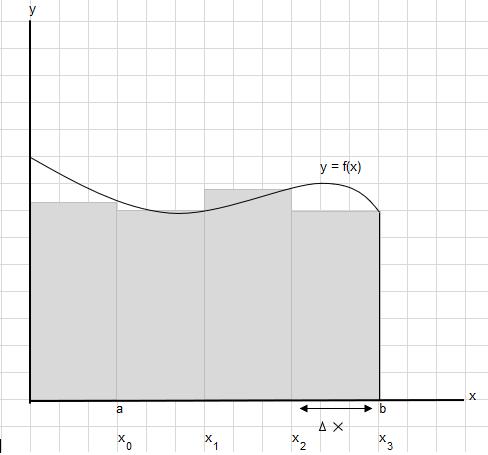
a और b के बीच के क्षेत्र को समान खंडों में विभाजित करें जैसे कि प्रत्येक आयत की चौड़ाई \(\Delta x\) हो।
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
इन आयतों के क्षेत्रफल का योग \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) के रूप में लिखा जा सकता है।
हम क्षेत्र का एक बेहतर अनुमान लगा सकते हैं क्योंकि \(\Delta x \) छोटा हो जाता है या दूसरे शब्दों में जब कई खंडों में वृद्धि होती है। तो \(\Delta x \) पतला और पतला हो जाता है और n बड़ा और बड़ा हो जाता है। बेहतर सन्निकटन प्राप्त करने की यह धारणा क्योंकि हम सीमा लेते हैं क्योंकि n अनंत तक पहुंचता है और \(\Delta x \) असीम रूप से छोटा होता जा रहा है, इंटीग्रल है।
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) x के f के अंतर्गत x = a और x = b के बीच के क्षेत्र को दर्शाता है
समाकलन ढूँढना, संजात ढूँढने का उल्टा है।
x 2 का अवकलज 2x है। अतः 2x का समाकल x 2 है।
\(\int 2x \space dx = x^2 + C\) , जहां सी एक स्थिरांक है। चूँकि अचर का अवकलज 0 है, इसलिए x 2 , x 2 +4, x 2 +10, x 2 +99 का अवकलज 2x है। अतः 2x का समाकल x 2 +C होता है।
आइए सामान्य कार्यों के अभिन्न को देखें:
| सामान्य कार्य | समारोह | अभिन्न |
| नियत | \(\int a \cdot dx\) | \(ax + c\) |
| चर | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| वर्ग | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| घातीय | \(\int e^x \cdot dx\) | \(e^x + c\) |
| त्रिकोणमिति(x रेडियन में) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
सामान्य एकीकरण नियम:
| नियम | समारोह | अभिन्न |
| स्थिरांक से गुणन | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| पावर नियम (एन <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| योग नियम | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| अंतर नियम | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
इंटीग्रल की कक्षाएं
\(\int f(x) \space dx\) अनिश्चित समाकल का प्रतिनिधित्व करता है और \(\int_a^bf(x) \cdot dx\) एक निश्चित समाकल का प्रतिनिधित्व करता है। एक निश्चित समाकल के प्रारंभ और अंत मान होते हैं। यहाँ a और b को सीमाएँ या सीमाएँ कहते हैं। अनिश्चितकालीन अभिन्न एकीकरण का एक सामान्य रूप है और इसे फ़ंक्शन के व्युत्पन्न विरोधी के रूप में व्याख्या किया जा सकता है।
हम अनिश्चित समाकलन को a , और b पर, फिर घटाकर परिकलित करके निश्चित समाकलन पाते हैं। आइए इसे एक उदाहरण से समझते हैं:
हम जानते हैं \(\int 2x \cdot dx = x^2 + C\) । एक निश्चित समाकल \(\int _1^2 2x \cdot dx \) का मान क्या होगा?
x =1 पर, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2 पर, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
घटाना (4 + C) - (1 + C) = 3
\(\int _1^2 2x \cdot dx \) = 3 . का मान