Naučit ćeš:
Integrali zajedno s derivacijama temeljni su objekti u računanju. Proces izračunavanja integrala naziva se integracija , a približno izračunavanje integrala naziva se numerička integracija.
Postoje dvije klase integrala - određeni integral (kao 5) i neodređeni integrali, koji ima donju i gornju granicu kao \(\int_a^bf(x) \cdot dx\) .
Što je Integral?
Recimo da moramo pronaći površinu ispod krivulje i gornju x-os.
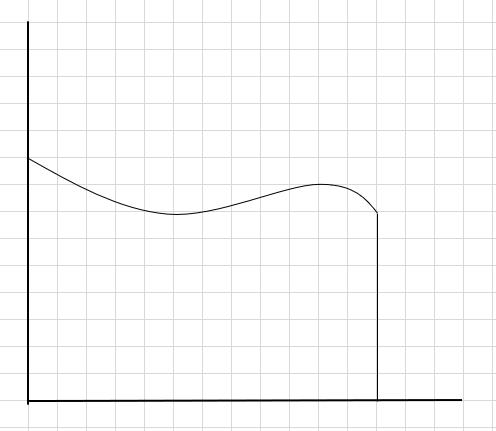
Jedan od načina za to je podijeliti regiju na četiri segmenta, a zatim nacrtati pravokutnik (koristeći ovu segmentnu liniju) tako da gornji desni kut svakog pravokutnika dodiruje krivulju (kao što je navedeno u nastavku)
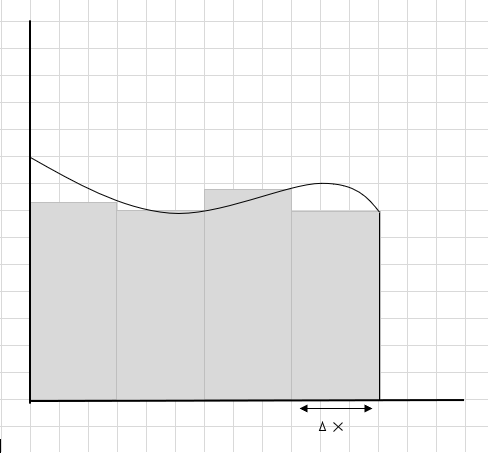
Zbroj površina ovih pravokutnih segmenata je procijenjena površina ispod ove krivulje. \(\Delta x \) je širina pravokutnika/kriški. Što mislite o procijenjenoj površini?
Veliki dio krivulje je propušten i nekoliko dodatnih dijelova se uzima u obzir prilikom izračunavanja površine ove regije krivulje. Prijava ispod slike tamno siva regija predstavlja promašaj i dodatne dijelove.
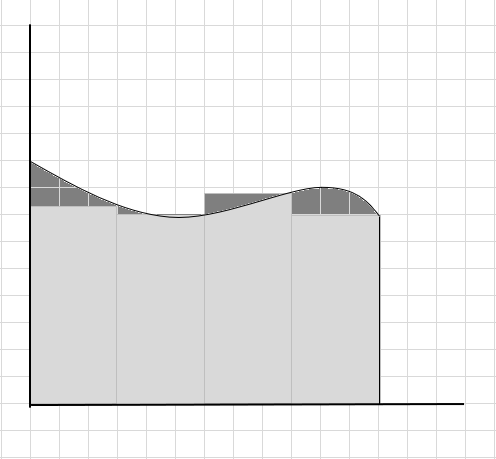
Možemo reći da je ovo loša procjena površine zakrivljenog područja jer se pravokutnici ne uklapaju točno ispod krivulje. Podijelimo površinu ispod ove krivulje na manje segmente.
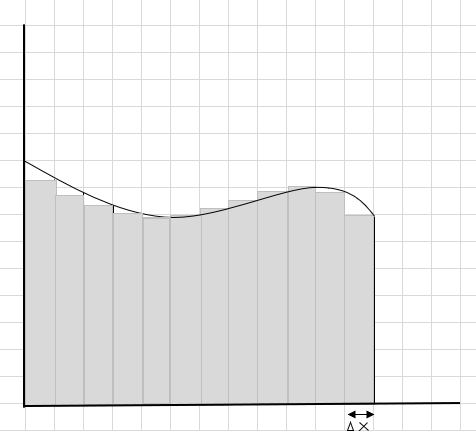
Možete vidjeti da se ovi pravokutnici bolje uklapaju unutar zakrivljenog područja od većih pravokutnih segmenata. Pokušajmo ovu zakrivljenu regiju podijeliti na manje segmente/kriške i pokušati odrediti površinu ispod krivulje.
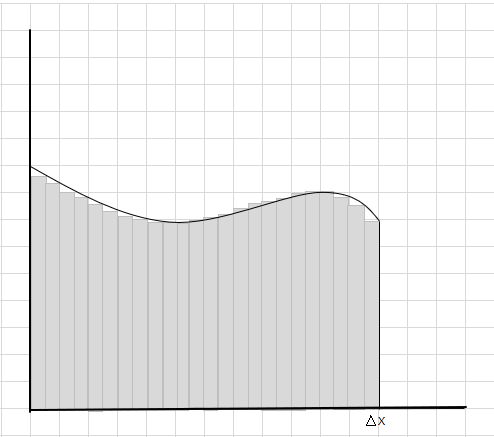
Promašaji i dodatni dijelovi postupno se smanjuju i pravokutnici se puno bolje uklapaju unutar regije krivulje. Možemo zaključiti da zbroj površina svih ovih pravokutnika daje dobru procjenu površine ispod krivulje. Ili drugim riječima, možemo reći kako se kriške približavaju nuli po širini odgovor se približava istinitom odgovoru. Sada pišemo dx za \(\Delta x\) da znači da se širina približava nuli.
Izvedimo formulu za integralni račun ovdje:
Recimo da trebamo pronaći površinu ispod ove krivulje između točaka a i b: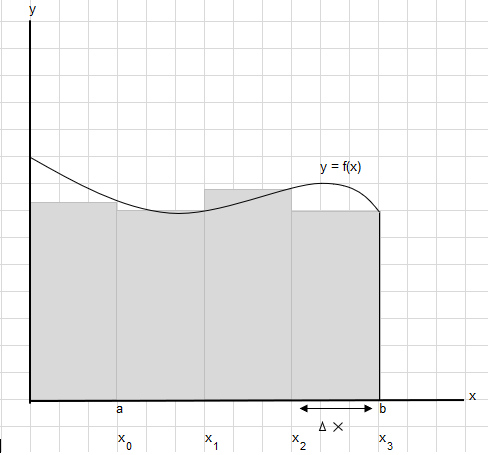
Podijelite područje između a i b na jednake segmente tako da širina svakog pravokutnika bude \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Zbroj površina ovih pravokutnika može se napisati kao \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Možemo imati bolju aproksimaciju površine kako se \(\Delta x \) smanjuje ili drugim riječima kada se broj segmenata povećava. Dakle, \(\Delta x \) postaje sve tanji i tanji, a n postaje sve veći i veći. Ovaj pojam dobivanja bolje aproksimacije dok uzimamo granicu kako se n približava beskonačnosti i \(\Delta x \) postaje beskonačno mali je Integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) predstavlja površinu ispod f od x između x = a i x = b
Pronalaženje integrala je obrnuto od pronalaženja izvedenica.
Derivat od x 2 je 2x. Dakle, integral od 2x je x 2 .
\(\int 2x \space dx = x^2 + C\) , gdje je C konstanta. Kako je derivacija konstante 0, stoga je derivacija x 2 , x 2 +4, x 2 +10, x 2 +99 2x. Stoga je integral od 2x x 2 +C.
Pogledajmo integrale uobičajenih funkcija:
| Uobičajene funkcije | Funkcija | Sastavni |
| Konstantno | \(\int a \cdot dx\) | \(ax + c\) |
| Varijabilna | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Kvadrat | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Eksponencijalno | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometrija (x u radijanima) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Uobičajena pravila integracije:
| Pravila | Funkcija | Sastavni |
| Množenje konstantom | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Pravilo snage (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Pravilo zbroja | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Pravilo razlike | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Klase integrala
\(\int f(x) \space dx\) predstavlja neodređeni integral, a \(\int_a^bf(x) \cdot dx\) predstavlja određeni integral. Određeni integral ima početnu i krajnju vrijednost. Ovdje se a i b nazivaju granicama ili granicama. Neodređeni integral je više opći oblik integracije i može se tumačiti kao antiderivat funkcije.
Definitivni integral nalazimo izračunavanjem neodređenog integrala na a , i na b , a zatim oduzimanjem. Shvatimo to na primjeru:
Znamo \(\int 2x \cdot dx = x^2 + C\) . Kolika će biti vrijednost određenog integrala \(\int _1^2 2x \cdot dx \) ?
Kod x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Kod x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Oduzmite (4 + C) - (1 + C) = 3
Vrijednost \(\int _1^2 2x \cdot dx \) = 3