Anda akan belajar:
Integral bersama dengan turunan adalah objek fundamental dalam kalkulus. Proses komputasi integral disebut integrasi dan perhitungan perkiraan integral disebut sebagai integrasi numerik.
Ada dua kelas integral - integral pasti (seperti 5) dan integral tak tentu, yang memiliki batas bawah dan atas seperti \(\int_a^bf(x) \cdot dx\) .
Apa itu integral?
Misalkan kita harus mencari luas di bawah kurva dan sumbu x di atas.
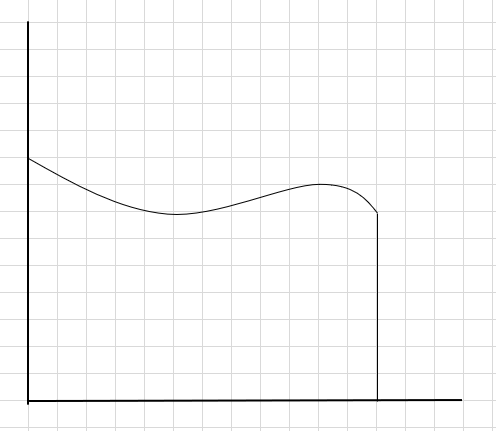
Salah satu cara untuk melakukannya adalah membagi wilayah menjadi empat segmen dan kemudian menggambar persegi panjang (menggunakan garis segmen ini) sedemikian rupa sehingga sudut kanan atas setiap persegi panjang menyentuh kurva (seperti yang diberikan di bawah ini)
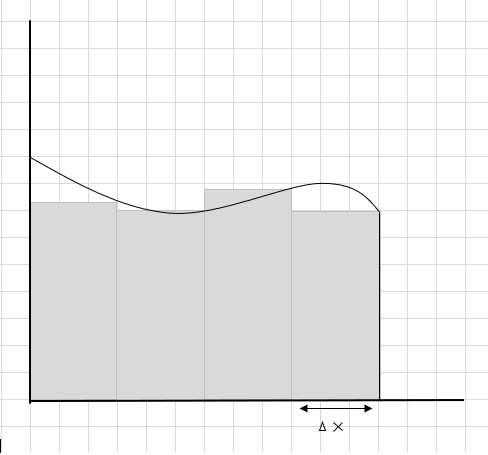
Jumlah luas segmen persegi panjang ini adalah perkiraan luas di bawah kurva ini. \(\Delta x \) menjadi lebar persegi panjang/irisan. Apa pendapat Anda tentang perkiraan luas?
Banyak bagian kurva yang terlewatkan dan beberapa bagian tambahan dipertimbangkan saat menghitung luas daerah kurva ini. Check-in di bawah gambar wilayah abu-abu gelap mewakili bagian yang terlewatkan dan bagian tambahan.
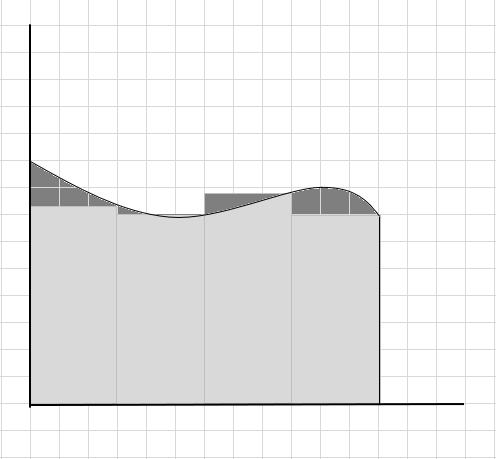
Kita dapat mengatakan ini adalah perkiraan yang buruk dari luas daerah yang melengkung karena persegi panjang tidak pas di bawah kurva. Mari kita bagi area di bawah kurva ini menjadi segmen-segmen yang lebih kecil.
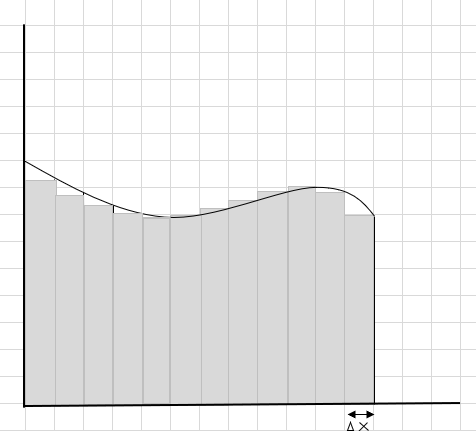
Anda dapat melihat bahwa persegi panjang ini lebih pas di dalam area lengkung daripada segmen persegi panjang yang lebih besar. Mari kita coba membagi daerah lengkung ini menjadi segmen/irisan yang lebih kecil dan mencoba menentukan luas di bawah kurva.
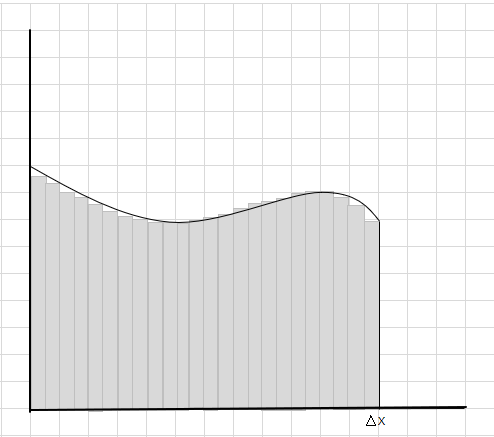
Bagian yang terlewat dan bagian tambahan secara bertahap berkurang dan persegi panjang lebih pas di dalam area kurva. Kita dapat menyimpulkan bahwa jumlah luas semua persegi panjang ini memberikan perkiraan yang baik untuk luas di bawah kurva. Atau dengan kata lain, kita dapat mengatakan ketika lebar irisan mendekati nol, jawabannya mendekati jawaban yang sebenarnya. Kita sekarang menulis dx untuk \(\Delta x\) yang berarti lebarnya mendekati nol.
Mari kita turunkan rumus kalkulus integral di sini:
Katakanlah kita perlu mencari luas di bawah kurva ini antara titik a dan b: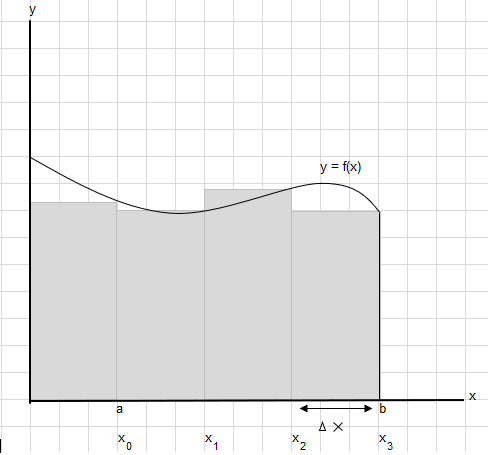
Bagilah luas antara a dan b menjadi segmen yang sama sehingga lebar setiap persegi panjang adalah \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Jumlah luas persegi panjang ini dapat ditulis sebagai \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Kita dapat memiliki perkiraan luas yang lebih baik karena \(\Delta x \) semakin kecil atau dengan kata lain ketika sejumlah segmen bertambah. Jadi \(\Delta x \) menjadi lebih tipis dan lebih tipis dan n menjadi lebih besar dan lebih besar. Gagasan untuk mendapatkan perkiraan yang lebih baik saat kita mengambil batas ketika n mendekati tak terhingga dan \(\Delta x \) menjadi sangat kecil adalah Integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) menyatakan luas di bawah f dari x antara x = a dan x = b
Mencari Integral adalah kebalikan dari mencari Derivatif.
Turunan dari x 2 adalah 2x. Jadi integral dari 2x adalah x 2 .
\(\int 2x \space dx = x^2 + C\) , di mana C adalah konstanta. Karena turunan dari konstanta adalah 0 maka turunan dari x 2 , x 2 +4, x 2 +10, x 2 +99 adalah 2x. Jadi integral dari 2x adalah x 2 +C.
Mari kita lihat integral dari fungsi umum:
| Fungsi Umum | Fungsi | Integral |
| Konstan | \(\int a \cdot dx\) | \(ax + c\) |
| Variabel | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Persegi | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Eksponensial | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometri (x dalam radian) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Aturan Integrasi Umum:
| Aturan | Fungsi | Integral |
| Perkalian dengan konstanta | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Aturan Pangkat(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Aturan Jumlah | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Aturan Perbedaan | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Kelas Integral
\(\int f(x) \space dx\) menyatakan integral tak tentu dan \(\int_a^bf(x) \cdot dx\) menyatakan integral tertentu. Integral pasti memiliki nilai awal dan akhir. Disini a dan b disebut limit atau batasan. Integral tak tentu lebih merupakan bentuk integral umum dan dapat diartikan sebagai antiturunan dari fungsi.
Kita mencari Integral Tentu dengan menghitung Integral tak tentu pada a , dan pada b , lalu mengurangkannya. Mari kita pahami ini dengan sebuah contoh:
Kita tahu \(\int 2x \cdot dx = x^2 + C\) . Berapakah nilai integral tertentu \(\int _1^2 2x \cdot dx \) ?
Pada x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Pada x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Kurangi (4 + C) - (1 + C) = 3
Nilai dari \(\int _1^2 2x \cdot dx \) = 3