Imparerai:
Gli integrali insieme alle derivate sono gli oggetti fondamentali nel calcolo. Il processo di calcolo di un integrale è chiamato integrazione e il calcolo approssimativo di un integrale è definito integrazione numerica.
Esistono due classi di integrali: integrale definito (come 5) e integrali indefiniti, che ha limiti inferiore e superiore come \(\int_a^bf(x) \cdot dx\) .
Cos'è Integrale?
Diciamo che dobbiamo trovare l'area sotto la curva e l'asse x sopra.
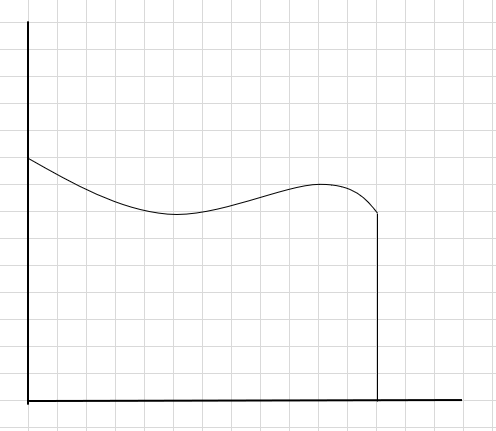
Un modo per farlo è dividere la regione in quattro segmenti e quindi disegnare un rettangolo (usando questa linea di segmento) in modo tale che l'angolo in alto a destra di ogni rettangolo tocchi la curva (come indicato di seguito)
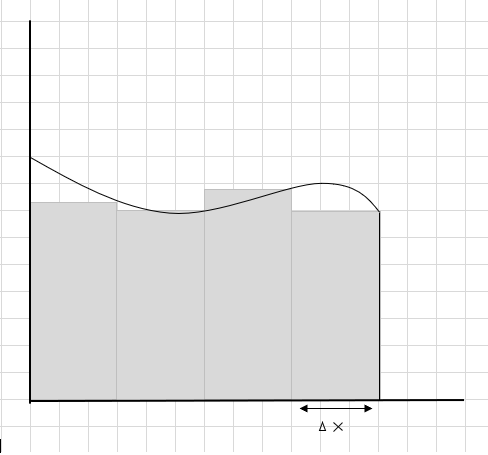
La somma dell'area di questi segmenti rettangolari è l'area stimata sotto questa curva. \(\Delta x \) è la larghezza dei rettangoli/fette. Cosa ne pensi dell'area stimata?
Molte parti della curva vengono perse e alcune parti aggiuntive vengono considerate durante il calcolo dell'area di questa regione della curva. Il check-in sotto l'immagine la regione grigio scuro rappresenta parti mancanti e aggiuntive.
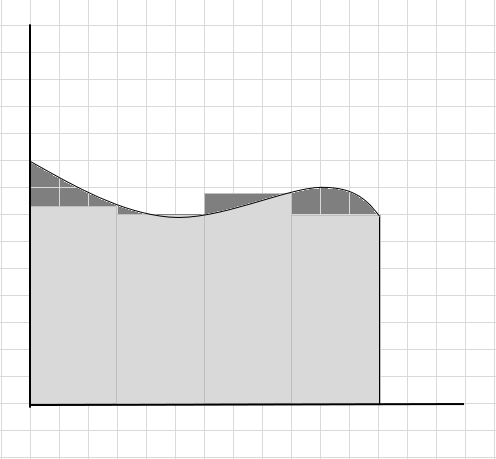
Possiamo dire che questa è una stima scadente dell'area della regione curva poiché i rettangoli non si adattano esattamente sotto la curva. Dividiamo l'area sotto questa curva in segmenti più piccoli.
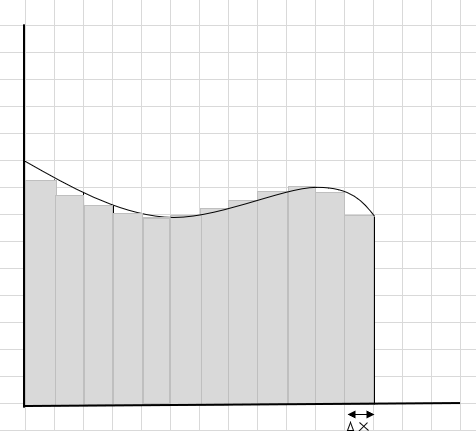
Puoi vedere che questi rettangoli si adattano all'interno dell'area curva meglio dei segmenti rettangolari più grandi. Proviamo a dividere questa regione curva in segmenti/fette più piccoli e proviamo a determinare l'area sotto la curva.
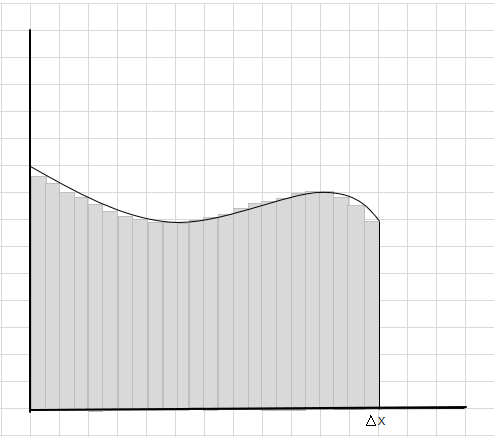
Le parti mancanti e extra si stanno gradualmente riducendo e i rettangoli si adattano molto meglio all'interno della regione della curva. Possiamo dedurre che la somma dell'area di tutti questi rettangoli fornisce una buona stima dell'area sotto la curva. O in altre parole, possiamo dire che quando le fette si avvicinano allo zero in larghezza la risposta si avvicina alla risposta vera. Ora scriviamo dx per \(\Delta x\) a significa che la larghezza si avvicina allo zero.
Deriviamo qui la formula per il calcolo integrale:
Diciamo che dobbiamo trovare l'area sotto questa curva tra i punti a e b: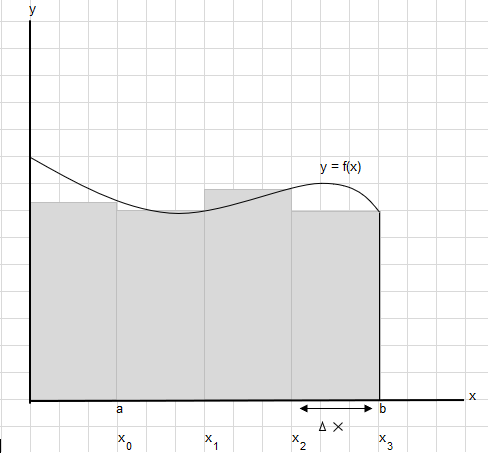
Dividi l'area tra a e b in segmenti uguali in modo tale che la larghezza di ciascun rettangolo sia \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
La somma dell'area di questi rettangoli può essere scritta come \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Possiamo avere una migliore approssimazione dell'area man mano che \(\Delta x \) diminuisce o in altre parole quando aumenta un numero di segmenti. Quindi \(\Delta x \) diventa sempre più sottile e n diventa sempre più grande. Questa nozione di ottenere una migliore approssimazione quando prendiamo il limite quando n si avvicina all'infinito e \(\Delta x \) diventa infinitamente piccolo è Integrale.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) rappresenta l'area sotto f di x tra x = a e x = b
Trovare l'integrale è l'opposto di trovare le derivate.
La derivata di x 2 è 2x. Quindi un integrale di 2x è x 2 .
\(\int 2x \space dx = x^2 + C\) , dove C è una costante. Poiché la derivata della costante è 0, la derivata di x 2 , x 2 +4, x 2 +10, x 2 +99 è 2x. Quindi l'integrale di 2x è x 2 +C.
Diamo un'occhiata agli integrali delle funzioni comuni:
| Funzioni comuni | Funzione | Integrante |
| Costante | \(\int a \cdot dx\) | \(ax + c\) |
| Variabile | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Piazza | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Esponenziale | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometria (x in radianti) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Regole di integrazione comuni:
| Regole | Funzione | Integrante |
| Moltiplicazione per costante | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Regola di potenza(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Regola della somma | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Regola della differenza | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Classi di integrali
\(\int f(x) \space dx\) rappresenta l'integrale indefinito e \(\int_a^bf(x) \cdot dx\) rappresenta un integrale definito. Un integrale definito ha valori iniziali e finali. Qui a e b sono chiamati limiti o confini. L'integrale indefinito è più una forma generale di integrazione e può essere interpretato come anti-derivata della funzione.
Troviamo l'integrale definito calcolando l'integrale indefinito in a e in b , quindi sottraendo. Cerchiamo di capirlo con un esempio:
Sappiamo \(\int 2x \cdot dx = x^2 + C\) . Quale sarà il valore di un integrale definito \(\int _1^2 2x \cdot dx \) ?
In x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
In x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Sottrai (4 + C) - (1 + C) = 3
Valore di \(\int _1^2 2x \cdot dx \) = 3