学習内容:
積分と導関数は、微積分の基本的なオブジェクトです。積分を計算するプロセスは積分と呼ばれ、積分の近似計算は数値積分と呼ばれます。
積分には 2 つのクラスがあります。定積分 (5 など) と、 \(\int_a^bf(x) \cdot dx\)のように下限と上限がある不定積分です。
インテグラルとは?
曲線の下の領域と上の x 軸を見つける必要があるとしましょう。
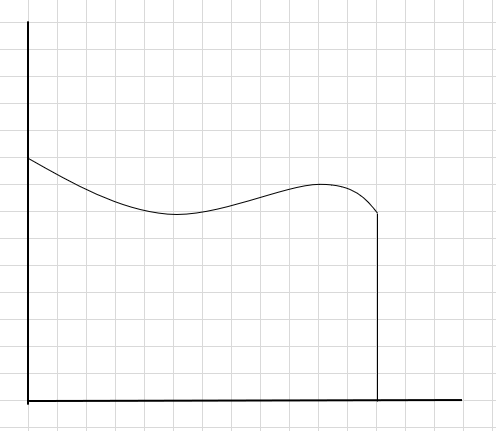
1 つの方法は、領域を 4 つのセグメントに分割し、(このセグメント ラインを使用して) 四角形を描画して、各四角形の右上隅が曲線に接触するようにすることです (以下に示すように)。
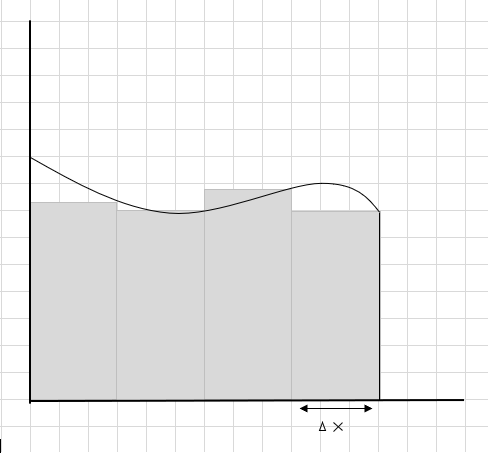
これらの長方形セグメントの面積の合計は、この曲線の下の推定面積です。 \(\Delta x \)は長方形/スライスの幅です。推定面積についてどう思いますか?
多くの曲線部分が見落とされ、この曲線領域の面積を計算する際にいくつかの追加部分が考慮されます。画像の下のチェックイン ダーク グレーの領域は、欠落と追加パーツを表します。
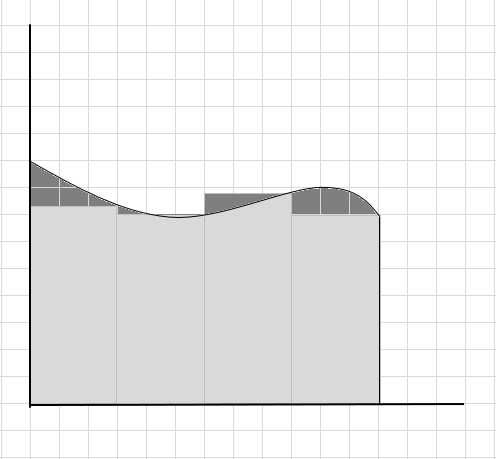
長方形は曲線の下に正確に収まらないため、これは曲線領域の面積の推定としては不十分であると言えます。この曲線の下の領域を小さなセグメントに分割しましょう。
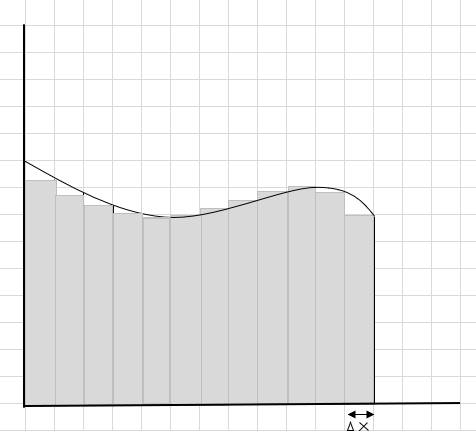
これらの四角形は、大きな四角形セグメントよりも曲面領域内に収まっていることがわかります。この曲線領域を小さなセグメント/スライスに分割して、曲線の下の領域を決定してみましょう。
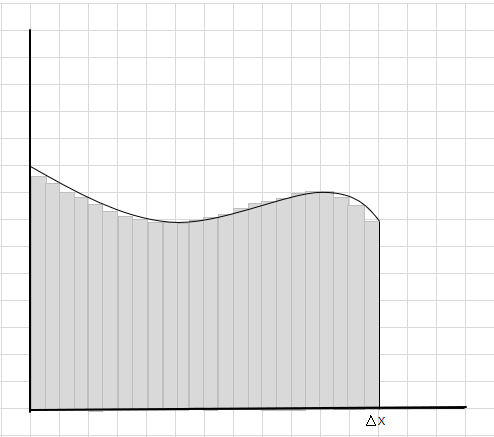
欠落部分と余分な部分は徐々に減少し、長方形は曲線領域内によりよく適合しています。これらすべての長方形の面積の合計が、曲線の下の面積の適切な推定値になると推測できます。言い換えれば、スライスの幅がゼロに近づくにつれて、答えは真の答えに近づくと言えます。 \(\Delta x\)を dx と書き、幅がゼロに近づいていることを意味します。
ここで積分計算の式を導き出しましょう。
点aとbの間のこの曲線の下の領域を見つける必要があるとしましょう: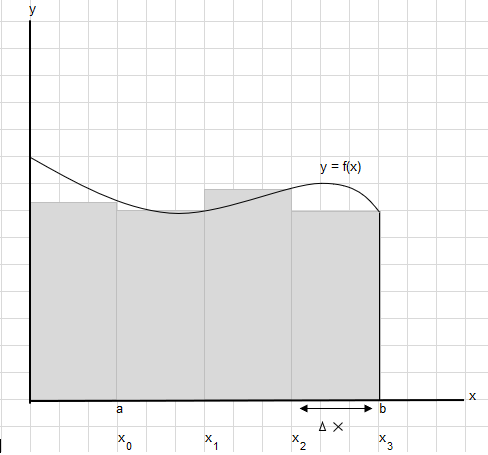
各長方形の幅が\(\Delta x\)になるように、a と b の間の領域を均等なセグメントに分割します。
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
これらの長方形の面積の合計\(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\)書くことができます。
\(\Delta x \)が小さくなるほど、つまりセグメントの数が増えるほど、面積の近似値が高くなります。したがって、 \(\Delta x \)ますます薄くなり、n はますます大きくなります。 n が無限大に近づき\(\Delta x \)が無限に小さくなるにつれて極限をとることで、より良い近似が得られるというこの概念は、Integral です。
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) x = a と x = b の間の x の f の下の領域を表します
積分を見つけることは、導関数を見つけることの逆です。
x 2の導関数は 2x です。したがって、2x の積分は x 2です。
\(\int 2x \space dx = x^2 + C\) 、C は定数です。定数の導関数は 0 なので、x 2 、x 2 +4、x 2 +10、x 2 +99 の導関数は 2x です。したがって、2x の積分は x 2 +C です。
一般的な関数の積分を見てみましょう:
| 共通機能 | 関数 | 積分 |
| 絶え間ない | \(\int a \cdot dx\) | \(ax + c\) |
| 変数 | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| 四角 | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| 指数関数的 | \(\int e^x \cdot dx\) | \(e^x + c\) |
| 三角法 (x はラジアン) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
一般的な統合ルール:
| ルール | 関数 | 積分 |
| 定数による乗算 | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| パワールール(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| 合計ルール | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| 差分ルール | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
積分のクラス
\(\int f(x) \space dx\)は不定積分を表し、 \(\int_a^bf(x) \cdot dx\)定積分を表します。定積分には開始値と終了値があります。ここで a と b は極限または境界と呼ばれます。不定積分は、より一般的な形の積分であり、関数の反導関数として解釈できます。
定積分は、 aとbで不定積分を計算してから減算することで求められます。例でこれを理解しましょう:
\(\int 2x \cdot dx = x^2 + C\)知っています。定積分\(\int _1^2 2x \cdot dx \)の値は?
x =1 では、 \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2 では、 \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
減算 (4 + C) - (1 + C) = 3
\(\int _1^2 2x \cdot dx \)の値 = 3