Ти ќе научиш:
Интегралите заедно со дериватите се основните објекти во пресметката. Процесот на пресметување на интеграл се нарекува интеграција , а приближното пресметување на интеграл се нарекува нумеричка интеграција.
Постојат две класи на интеграли - определени интеграли (како 5) и неопределени интеграли, кои имаат долни и горни граници како \(\int_a^bf(x) \cdot dx\) .
Што е интегрално?
Да речеме дека треба да ја најдеме областа под кривата и горната х-оска.
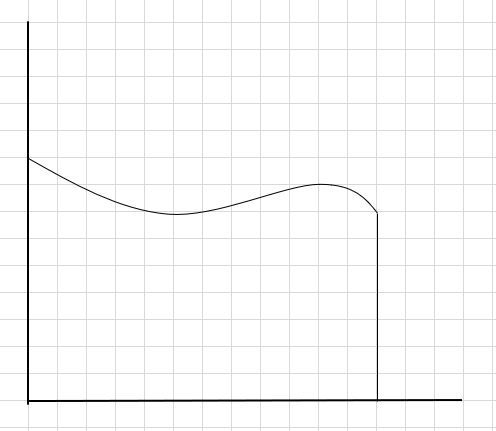
Еден начин да се направи е да се подели регионот на четири отсечки и потоа да се нацрта правоаголник (користејќи ја оваа отсечка линија) така што горниот десен агол на секој правоаголник ќе ја допира кривата (како што е дадено подолу)
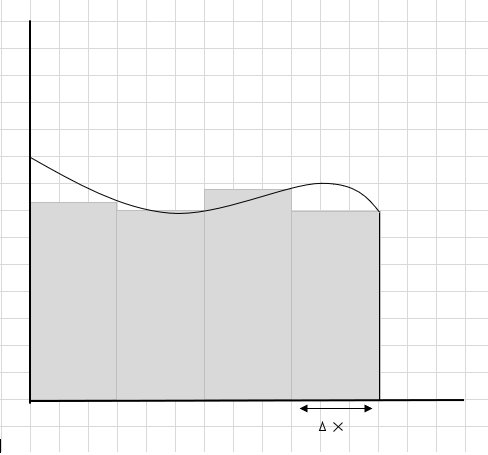
Збирот на плоштината на овие правоаголни отсечки е проценетата површина под оваа крива. \(\Delta x \) е ширината на правоаголниците/парчињата. Што мислите за проценетата површина?
Многу кривини се пропуштени и се земаат предвид неколку дополнителни делови при пресметувањето на површината на овој кривичен регион. Пријавувањето подолу на сликата темно сива област претставува пропуштени и дополнителни делови.
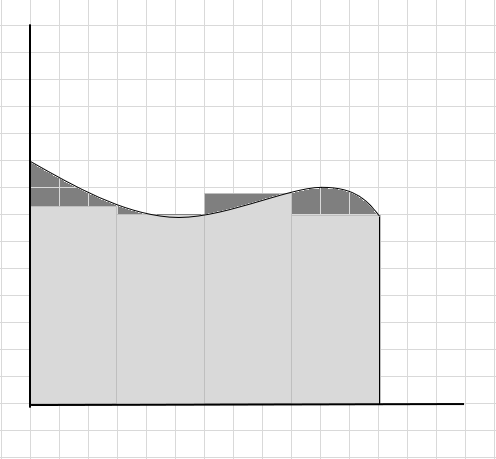
Можеме да кажеме дека ова е лоша проценка на површината на кривиот регион бидејќи правоаголниците не се вклопуваат точно под кривата. Ајде да ја поделиме областа под оваа крива на помали сегменти.
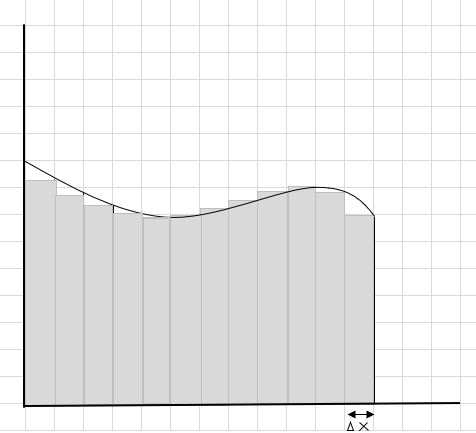
Можете да видите дека овие правоаголници се вклопуваат во закривената област подобро од поголемите правоаголни сегменти. Ајде да се обидеме да го поделиме овој закривен регион на помали сегменти/парчиња и да се обидеме да ја одредиме областа под кривата.
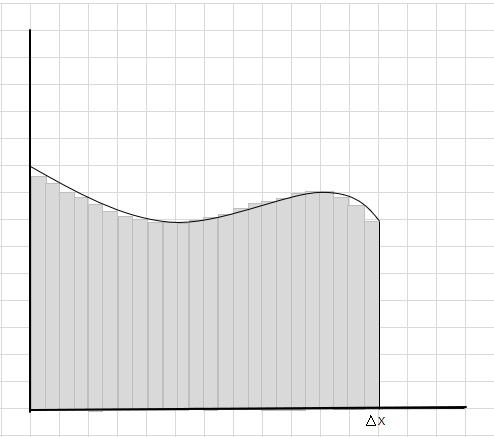
Промашувањето и дополнителните делови постепено се намалуваат, а правоаголниците многу подобро се вклопуваат во областа на кривата. Можеме да заклучиме дека збирот на плоштината на сите овие правоаголници дава добра проценка на површината под кривата. Или со други зборови, можеме да кажеме како што парчињата се приближуваат до нула во ширина, одговорот се приближува до вистинскиот одговор. Сега пишуваме dx за \(\Delta x\) да значи дека ширината се приближува до нула.
Ајде да ја изведеме формулата за интегрално пресметување овде:
Да речеме дека треба да ја најдеме областа под оваа крива помеѓу точките a и b: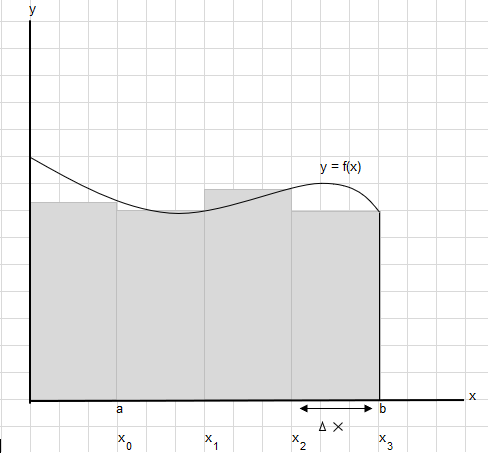
Поделете ја областа помеѓу a и b на еднакви отсечки така што ширината на секој правоаголник е \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Збирот на плоштината на овие правоаголници може да се запише како \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Можеме да имаме подобра апроксимација на плоштината кога \(\Delta x \) станува помала или со други зборови кога се зголемува бројот на сегменти. Така, \(\Delta x \) станува потенок и потенок, а n станува се поголем и поголем. Овој поим за добивање на подобра апроксимација кога ја земаме границата кога n се приближува до бесконечноста и \(\Delta x \) станува бесконечно мала е интегрален.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) ја претставува областа под f од x помеѓу x = a и x = b
Наоѓањето на интеграл е обратно од пронаоѓањето на деривати.
Изводот на x 2 е 2x. Значи интеграл од 2x е x 2 .
\(\int 2x \space dx = x^2 + C\) , каде што C е константа. Бидејќи изводот на константата е 0, оттука изводот на x 2 , x 2 +4, x 2 +10, x 2 +99 е 2x. Затоа интеграл на 2x е x 2 +C.
Да ги погледнеме интегралите на заедничките функции:
| Заеднички функции | Функција | Интегрален |
| Постојана | \(\int a \cdot dx\) | \(ax + c\) |
| Променлива | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Плоштад | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Експоненцијална | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Тригонометрија (x во радијани) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Заеднички правила за интеграција:
| Правила | Функција | Интегрален |
| Множење со константа | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Правило за напојување (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Правило за сума | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Правило за разлика | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Класи на интеграли
\(\int f(x) \space dx\) претставува неопределен интеграл и \(\int_a^bf(x) \cdot dx\) претставува определен интеграл. Дефинитивен интеграл има почетни и крајни вредности. Овде a и b се нарекуваат граници или граници. Неопределениот интеграл е повеќе општа форма на интеграција и може да се толкува како антидериват на функцијата.
Определениот интеграл го наоѓаме со пресметување на неопределениот интеграл на a , и на b , а потоа одземање. Да го разбереме ова со пример:
Знаеме \(\int 2x \cdot dx = x^2 + C\) . Која ќе биде вредноста на определен интеграл \(\int _1^2 2x \cdot dx \) ?
На x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
На x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Одземете (4 + C) - (1 + C) = 3
Вредност на \(\int _1^2 2x \cdot dx \) = 3