Та сурах болно:
Интеграл нь деривативын хамт тооцооллын үндсэн объект юм. Интегралыг тооцоолох үйл явцыг интеграл гэж нэрлэдэг ба интегралын ойролцоо тооцоог тоон интеграл гэж нэрлэдэг.
Интегралын хоёр ангилал байдаг - тодорхой интеграл (5 гэх мэт) ба тодорхойгүй интегралууд нь \(\int_a^bf(x) \cdot dx\) гэх мэт доод ба дээд хязгаартай.
Интеграл гэж юу вэ?
Муруй ба дээрх x тэнхлэгийн доорх талбайг олох ёстой гэж хэлье.
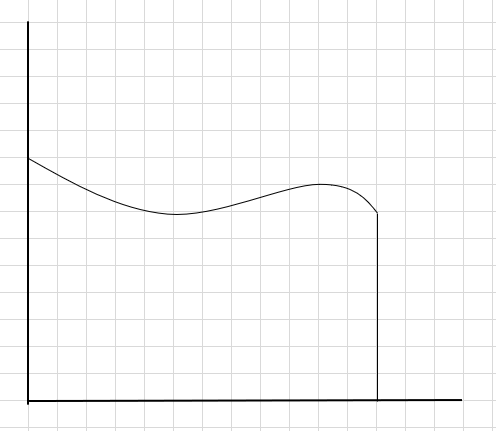
Хийх нэг арга бол тухайн бүс нутгийг дөрвөн сегмент болгон хувааж, дараа нь тэгш өнцөгт бүрийн баруун дээд булан муруйд хүрэхийн тулд (энэ сегментийн шугамыг ашиглан) тэгш өнцөгт зурах явдал юм.
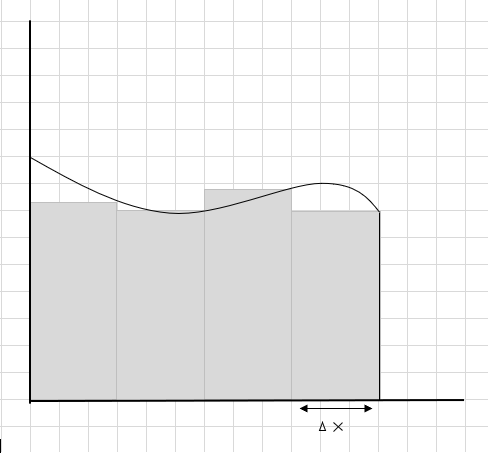
Эдгээр тэгш өнцөгт сегментүүдийн талбайн нийлбэр нь энэ муруйн доорх тооцоолсон талбай юм. \(\Delta x \) нь тэгш өнцөгт/зүсмэлийн өргөн юм. Тооцоолсон талбайн талаар та юу гэж бодож байна вэ?
Энэ муруйн бүсийн талбайг тооцоолохдоо маш олон муруйн хэсгийг орхигдуулж, хэд хэдэн нэмэлт хэсгийг харгалзан үзнэ. Доорх зургийн хар саарал бүс нь орхигдсон болон нэмэлт хэсгүүдийг илэрхийлдэг.
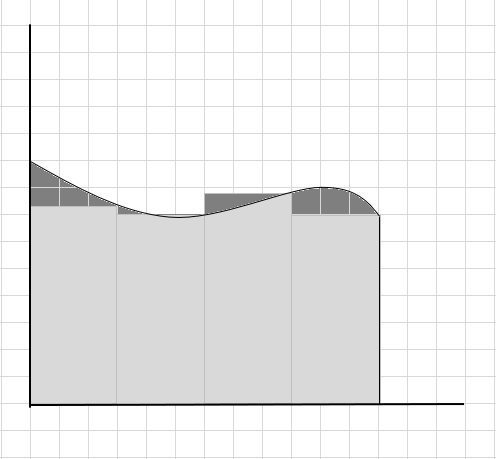
Тэгш өнцөгтүүд муруйн доор яг таарахгүй тул энэ нь муруй хэсгийн талбайн үнэлгээ муу байна гэж хэлж болно. Энэ муруйн доорх талбайг жижиг хэсгүүдэд хуваацгаая.
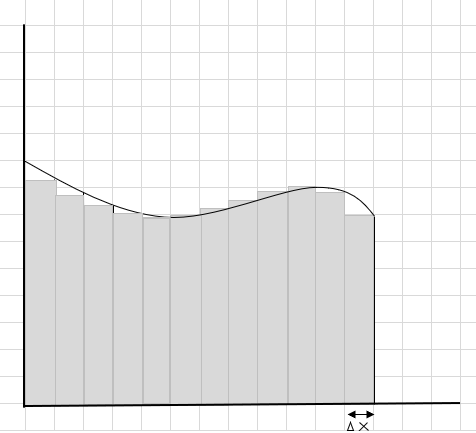
Эдгээр тэгш өнцөгтүүд нь том тэгш өнцөгт сегментүүдээс илүү муруй хэсэгт багтах болно. Энэ муруй мужийг жижиг хэсгүүд/зүсмэлүүд болгон хувааж, муруйн доорх талбайг тодорхойлохыг хичээцгээе.
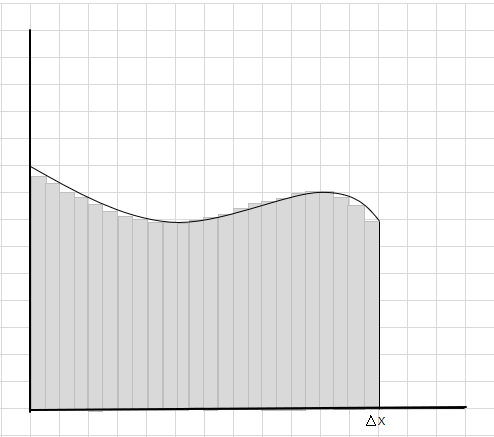
Алдагдсан болон нэмэлт хэсгүүд нь аажмаар багасч, тэгш өнцөгтүүд муруй хэсэгт илүү сайн таарч байна. Эдгээр бүх тэгш өнцөгтүүдийн талбайн нийлбэр нь муруйн доорх талбайг сайн тооцоолж чадна гэж бид дүгнэж болно. Өөрөөр хэлбэл, зүсмэлүүдийн өргөн тэг рүү ойртох тусам хариулт нь үнэн хариулт руу ойртоно гэж хэлж болно. Бид одоо \(\Delta x\) -д dx гэж бичээд өргөн нь тэг рүү ойртож байна гэсэн үг.
Интеграл тооцооллын томъёог эндээс гаргая.
Энэ муруй доорх талбайг a ба b цэгийн хооронд олох хэрэгтэй гэж хэлье.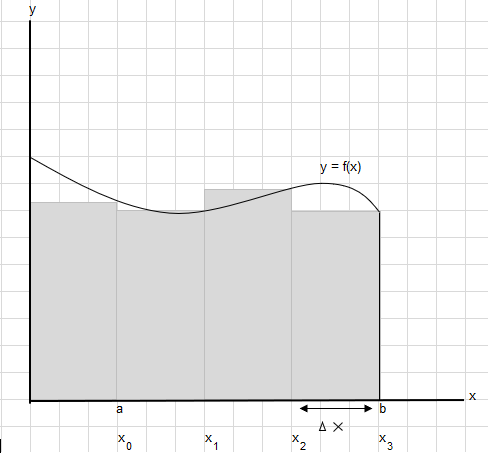
a ба b хоорондох талбайг тэгш өнцөгт бүрийн өргөн \(\Delta x\) байхаар тэнцүү хэсгүүдэд хуваа.
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Эдгээр тэгш өнцөгтүүдийн талбайн нийлбэрийг \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) гэж бичиж болно.
\(\Delta x \) багасах эсвэл өөрөөр хэлбэл сегментийн тоо нэмэгдэх үед бид талбайн хэмжээг илүү сайн ойртуулж чадна. Тиймээс \(\Delta x \) нимгэн, нарийсч, n нь улам томрох болно. n нь хязгааргүйд ойртож, \(\Delta x \) хязгааргүй жижиг болох үед бид хязгаарыг авах үед илүү сайн ойртуулах тухай ойлголт нь интеграл юм.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) нь x = a ба x = b хоорондох х-ийн f-ийн доорх талбайг илэрхийлнэ.
Интеграл олох нь дериватив олохын эсрэг үйлдэл юм.
x 2- ын дериватив нь 2x. Тэгэхээр 2x-ийн интеграл нь x 2 байна.
\(\int 2x \space dx = x^2 + C\) , энд C нь тогтмол байна. Тогтмолын дериватив нь 0 тул x 2 , x 2 +4, x 2 +10, x 2 +99 нь 2x-ийн дериватив юм. Тиймээс 2x-ийн интеграл нь x 2 +C байна.
Нийтлэг функцүүдийн интегралуудыг авч үзье.
| Нийтлэг функцууд | Чиг үүрэг | Интеграл |
| Тогтмол | \(\int a \cdot dx\) | \(ax + c\) |
| Хувьсагч | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Дөрвөлжин | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Экспоненциал | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Тригонометр (радианаар x) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Интеграцийн нийтлэг дүрмүүд:
| Дүрэм | Чиг үүрэг | Интеграл |
| Тогтмолоор үржүүлэх | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Эрчим хүчний дүрэм(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Нийлбэрийн дүрэм | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Ялгаатай дүрэм | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Интегралын ангиуд
\(\int f(x) \space dx\) нь тодорхойгүй интегралыг, \(\int_a^bf(x) \cdot dx\) нь тодорхой интегралыг илэрхийлнэ. Тодорхой интеграл нь эхлэл ба төгсгөлийн утгатай байдаг. Энд a, b-г хязгаар буюу хил гэж нэрлэдэг. Тодорхой бус интеграл нь интегралын ерөнхий хэлбэр бөгөөд функцийн эсрэг дериватив гэж ойлгож болно.
Тодорхой бус интегралыг a , ба b цэг дээр тооцоод, дараа нь хасах замаар тодорхой интегралыг олно. Үүнийг жишээгээр ойлгоцгооё.
\(\int 2x \cdot dx = x^2 + C\) гэдгийг бид мэднэ. Тодорхой интеграл \(\int _1^2 2x \cdot dx \) ямар байх вэ?
x =1 үед \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2 үед \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
(4 + С) - (1 + С) = 3-ыг хасна
\(\int _1^2 2x \cdot dx \) -ийн утга = 3