သင်ယူရလိမ့်မည်-
နိမိတ်လက္ခဏာများ နှင့် ပေါင်းစပ်ထားသော ပေါင်းစည်းမှု သည် ကုလ၏ အခြေခံအရာဝတ္ထုများဖြစ်သည်။ Integral တစ်ခုအား တွက်ချက်ခြင်းလုပ်ငန်းစဉ်ကို ပေါင်းစည်းခြင်း ဟုခေါ်ပြီး Integral တစ်ခု၏ အနီးစပ်ဆုံးတွက်ချက်ခြင်းကို ဂဏန်းပေါင်းစည်းခြင်းဟု ခေါ်သည်။
ပေါင်းစည်းမှု အမျိုးအစား နှစ်ခု ရှိသည် - အတိအကျ ပေါင်းစည်းခြင်း (5 ကဲ့သို့) နှင့် \(\int_a^bf(x) \cdot dx\) ကဲ့သို့ အောက်နှင့် အထက် ကန့်သတ်ချက်များ ရှိသည့် Indefinite integrals များ။
Integral ဆိုတာ ဘာလဲ။
မျဉ်းကွေးနှင့် အထက် x ဝင်ရိုးအောက် ဧရိယာကို ရှာရမည်ဟု ဆိုပါစို့။
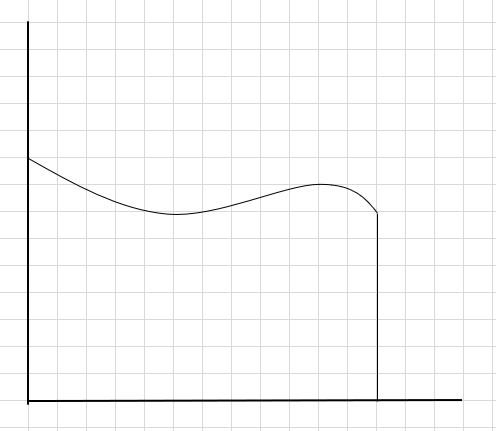
လုပ်ရန်တစ်နည်းမှာ ဧရိယာကို အပိုင်းလေးပိုင်းခွဲပြီး စတုဂံတစ်ခုစီ၏ အပေါ်ညာဘက်ထောင့်မှ မျဉ်းကွေးကိုထိသော စတုဂံတစ်ခု (ဤအပိုင်းမျဉ်းကို အသုံးပြု၍) စတုဂံတစ်ခုဆွဲပါ။
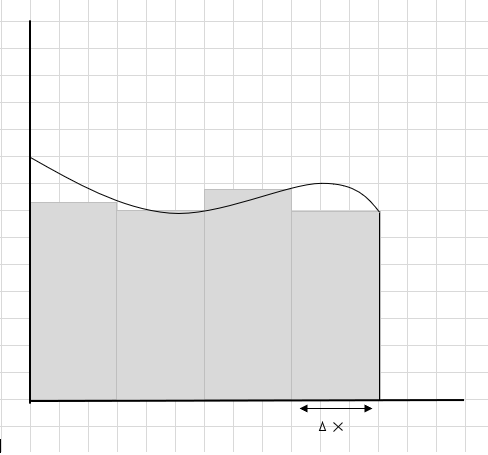
ဤစတုဂံအပိုင်းများ၏ ဧရိယာပေါင်းလဒ်သည် ဤမျဉ်းကွေးအောက်ရှိ ခန့်မှန်းဧရိယာဖြစ်သည်။ \(\Delta x \) သည် စတုဂံ/အချပ်များ၏ အကျယ်ဖြစ်သည်။ ခန့်မှန်းခြေဧရိယာကို သင်ဘယ်လိုထင်လဲ။
မျဉ်းကွေး အစိတ်အပိုင်း အများအပြား လွဲချော်နေပြီး ဤမျဉ်းကွေးဒေသ၏ ဧရိယာကို တွက်ချက်ရာတွင် နောက်ထပ် အစိတ်အပိုင်းအချို့ကို ထည့်သွင်းစဉ်းစားပါသည်။ ပုံအောက်ရှိ မီးခိုးရောင် အနက်ရောင် ဧရိယာသည် လွဲချော်မှုနှင့် နောက်ထပ် အစိတ်အပိုင်းများကို ကိုယ်စားပြုသည်။
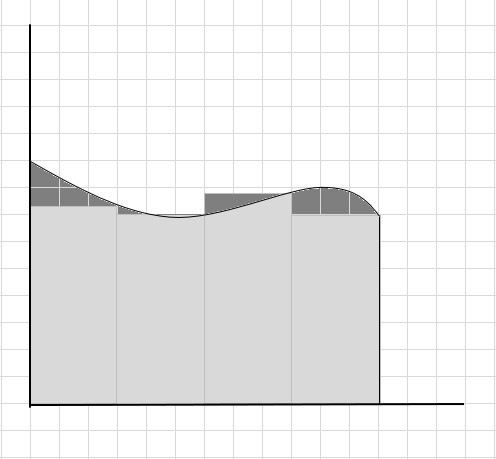
စတုဂံပုံများသည် မျဉ်းကွေးအောက်တွင် အတိအကျ မလိုက်ဖက်သောကြောင့် ကွေးညွှတ်သော ဧရိယာ၏ ဧရိယာကို ခန့်မှန်းခြေ ညံ့ဖျင်းသည်ဟု ကျွန်ုပ်တို့ပြောနိုင်သည်။ ဤမျဉ်းကွေးအောက်ရှိ ဧရိယာကို အပိုင်းငယ်များအဖြစ် ခွဲကြပါစို့။
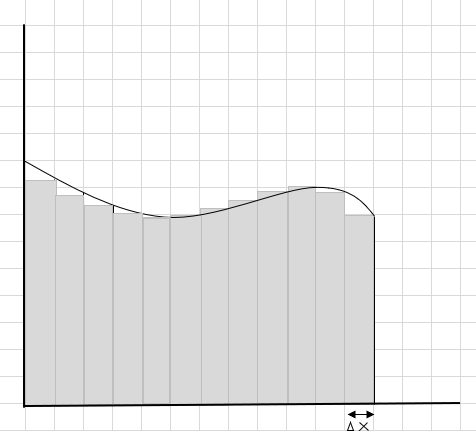
ဤစတုဂံများသည် ပိုကြီးသော စတုဂံအပိုင်းများထက် ကွေးသောဧရိယာအတွင်း၌ ပိုအဆင်ပြေကြောင်း သင်တွေ့နိုင်သည်။ ဤကွေးညွတ်သောဒေသကို သေးငယ်သောအပိုင်း/အချပ်များအဖြစ် ပိုင်းခြားပြီး မျဉ်းကွေးအောက်ရှိ ဧရိယာကို ဆုံးဖြတ်ရန် ကြိုးစားကြပါစို့။
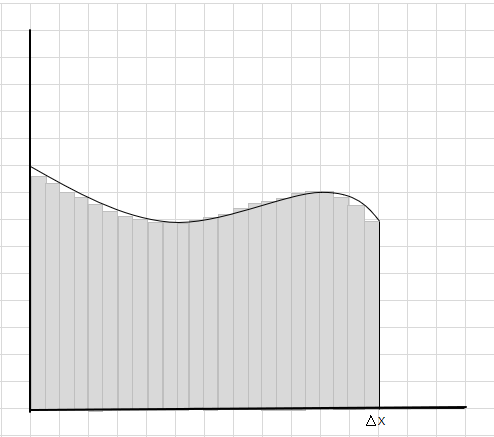
လွဲချော်မှုနှင့် အပိုအပိုင်းများသည် တဖြည်းဖြည်း လျှော့ချလာပြီး ထောင့်မှန်စတုဂံများသည် မျဉ်းကွေးဒေသအတွင်း ပိုကောင်းပါသည်။ ဤစတုဂံအားလုံး၏ ဧရိယာပေါင်းလဒ်ကို မျဉ်းကွေးအောက်ရှိ ဧရိယာ၏ ခန့်မှန်းချက်ကောင်းကောင်းပေးနိုင်သည်။ သို့မဟုတ် တစ်နည်းအားဖြင့် ဆိုရသော် အချပ်များသည် အကျယ် သုညသို့ ချဉ်းကပ်သောအခါ အဖြေသည် စစ်မှန်သော အဖြေဆီသို့ ချဉ်းကပ်လာသည်ဟု ဆိုနိုင်သည်။ အကျယ်သည် သုညသို့ ချဉ်းကပ်နေပြီဟု အဓိပ္ပါယ်ရသည့် \(\Delta x\) အတွက် dx ကို ရေးလိုက်ပါသည်။
ဤနေရာတွင် ပေါင်းစပ်တွက်ချက်မှုအတွက် ဖော်မြူလာကို ရယူကြပါစို့။
အမှတ် a နှင့် b ကြားရှိ ဤမျဉ်းကွေးအောက်တွင် ဧရိယာကို ရှာရန် လိုအပ်သည်ဟု ဆိုကြပါစို့။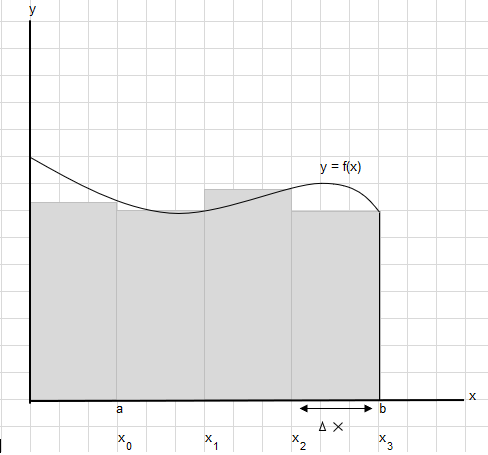
a နှင့် b အကြား ဧရိယာကို ထောင့်မှန်စတုဂံတစ်ခုစီ၏ အကျယ်သည် \(\Delta x\) ဖြစ်သည့်အတွက် အညီအမျှ အပိုင်းများခွဲပါ။
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
ဤစတုဂံများ၏ ဧရိယာ \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) အဖြစ် ရေးနိုင်သည်။
\(\Delta x \) သေးငယ်သွားခြင်းကြောင့် သို့မဟုတ် တစ်နည်းအားဖြင့် အပိုင်းများစွာ တိုးလာသောအခါတွင် ကျွန်ုပ်တို့သည် ပိုမိုကောင်းမွန်သော အနီးစပ်ဆုံး ဧရိယာကို ရရှိနိုင်ပါသည်။ ဒါကြောင့် \(\Delta x \) ပိုပါးလာပြီး ပိုပါးလာပြီး n ပိုကြီးလာမယ်။ n သည် အဆုံးမရှိ ချဉ်းကပ်လာသည်နှင့် \(\Delta x \) အဆုံးမရှိ သေးငယ်သွားသည်နှင့်အမျှ ကန့်သတ်ချက်ကို ယူလိုက်သည်နှင့် ပိုမိုကောင်းမွန်သော အနီးစပ်ဆုံး အယူအဆမှာ Integral ဖြစ်သည်။
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) x = a နှင့် x အကြား x = b ၏ f ၏ အောက်ဧရိယာကို ကိုယ်စားပြုသည်
Integral ကိုရှာဖွေခြင်းသည် Derivatives ရှာဖွေခြင်း၏ ပြောင်းပြန်ဖြစ်သည်။
x 2 ၏ ဆင်းသက်လာမှုသည် 2x ဖြစ်သည်။ ထို့ကြောင့် 2x ၏ integral သည် x 2 ဖြစ်သည်။
\(\int 2x \space dx = x^2 + C\) ၊ C သည် ကိန်းသေဖြစ်ပါသည်။ ကိန်းသေ၏ ဆင်းသက်လာခြင်းမှာ 0 ဖြစ်သောကြောင့် x 2၊ x 2 +4၊ x 2 +10၊ x 2 +99 သည် 2x ဖြစ်သည်။ ထို့ကြောင့် 2x သည် x 2 +C ဖြစ်သည်။
ဘုံလုပ်ဆောင်ချက်များ၏ အစိတ်အပိုင်းများကို ကြည့်ကြပါစို့။
| အသုံးများသောလုပ်ဆောင်ချက်များ | လုပ်ဆောင်ချက် | တစ်သားတည်း |
| စဉ်ဆက်မပြတ် | \(\int a \cdot dx\) | \(ax + c\) |
| ပြောင်းလဲနိုင်သော | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| ရင်ပြင် | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| ထပ်ကိန်း | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometry (ရေဒီယံတွင် x) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
ဘုံပေါင်းစပ်စည်းမျဉ်းများ-
| စည်းကမ်းများ | လုပ်ဆောင်ချက် | တစ်သားတည်း |
| ကိန်းသေဖြင့် မြှောက်ခြင်း။ | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| ပါဝါစည်းမျဉ်း(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| ပေါင်းလဒ်စည်းမျဉ်း | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| ကွာခြားမှု စည်းကမ်း | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Integrals အမျိုးအစားများ
\(\int f(x) \space dx\) indefinite integral ကို ကိုယ်စားပြုပြီး \(\int_a^bf(x) \cdot dx\) တိကျသော ပေါင်းစပ်မှုကို ကိုယ်စားပြုသည်။ တိကျသော ပေါင်းစပ်တစ်ခုတွင် အစနှင့်အဆုံးတန်ဖိုးများရှိသည်။ ဤနေရာတွင် a နှင့် b ကို limits သို့မဟုတ် boundaries ဟုခေါ်သည်။ indefinite integral သည် ပေါင်းစပ်မှု၏ ယေဘူယျပုံစံတစ်ခုဖြစ်ပြီး function ၏ anti-derivative အဖြစ် အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်ပါသည်။
ကျွန်ုပ်တို့သည် အကန့်အသတ်မရှိ Integral ကို a နှင့် b တွင် တွက်ချက်ပြီး နုတ်ယူခြင်းဖြင့် Definite Integral ကို ရှာဖွေသည်။ ဒါကို ဥပမာတစ်ခုနဲ့ နားလည်ကြပါစို့။
ငါတို့သိတာက \(\int 2x \cdot dx = x^2 + C\) ။ အတိအကျ ပေါင်းစပ်ထားသော တန်ဖိုးသည် အဘယ်နည်း \(\int _1^2 2x \cdot dx \) ။
x =1၊ \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2၊ \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
နုတ် (4 + C) - (1 + C) = 3
တန်ဖိုး၏ \(\int _1^2 2x \cdot dx \) = 3