तपाईंले सिक्नुहुनेछ:
डेरिभेटिभहरूका साथ एकीकृतहरू क्याल्कुलसका आधारभूत वस्तुहरू हुन्। अभिन्न गणना गर्ने प्रक्रियालाई एकीकरण भनिन्छ र पूर्णांकको अनुमानित गणनालाई संख्यात्मक एकीकरण भनिन्छ।
त्यहाँ दुईवटा वर्गहरू छन् - निश्चित पूर्णांक (जस्तै 5) र अनिश्चित पूर्णांक, जसको तल्लो र माथिल्लो सीमाहरू छन् जस्तै \(\int_a^bf(x) \cdot dx\)
Integral भनेको के हो?
मानौं हामीले वक्र मुनिको क्षेत्रफल र माथिको x-अक्ष पत्ता लगाउनु पर्छ।
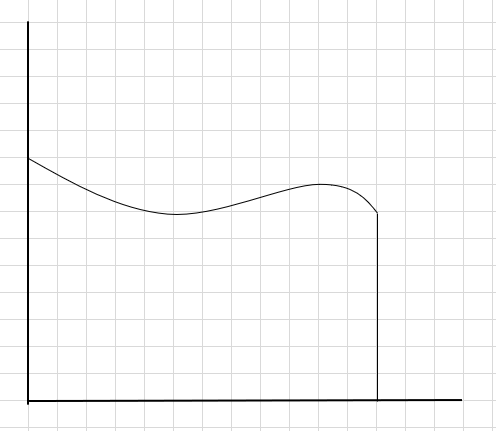
गर्ने एउटा तरिका भनेको क्षेत्रलाई चार खण्डमा विभाजन गर्नु हो र त्यसपछि एउटा आयत कोर्नुहोस् (यस खण्ड रेखा प्रयोग गरेर) जसरी प्रत्येक आयतको माथिल्लो दायाँ कुनाले वक्र छुन्छ (तल दिइएको छ)
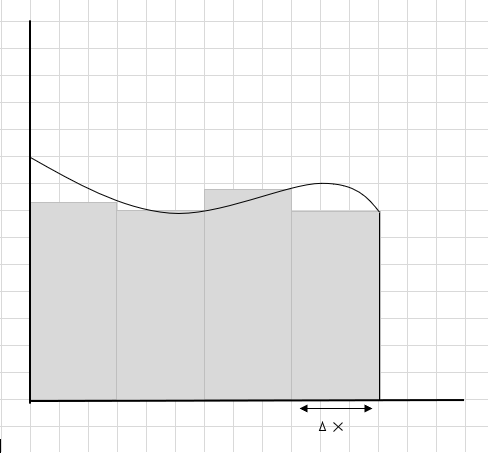
यी आयताकार खण्डहरूको क्षेत्रफलको योगफल यस वक्र अन्तर्गतको अनुमानित क्षेत्रफल हो। \(\Delta x \) आयत/स्लाइसहरूको चौडाइ हो। अनुमानित क्षेत्रफलको बारेमा तपाई के सोच्नुहुन्छ?
यो वक्र क्षेत्रको क्षेत्रफल गणना गर्दा धेरै वक्र भाग छुटेको छ र केही थप भागहरू विचार गरिन्छ। चेक-इन तल छवि गाढा खैरो क्षेत्र मिस आउट र अतिरिक्त भागहरू प्रतिनिधित्व गर्दछ।
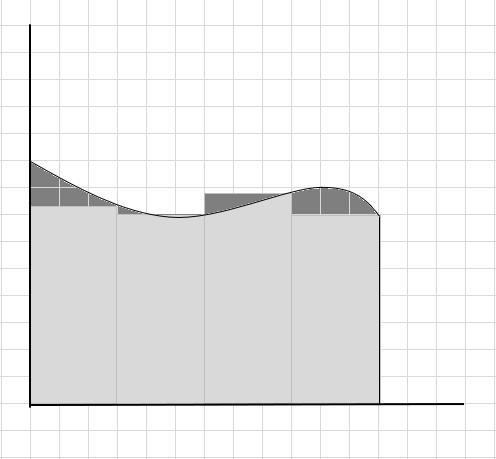
हामी भन्न सक्छौं कि यो वक्र क्षेत्रको क्षेत्रफलको कमजोर अनुमान हो किनभने आयतहरू वक्र मुनि ठ्याक्कै फिट हुँदैन। यस वक्र मुनिको क्षेत्रफललाई साना खण्डहरूमा विभाजन गरौं।
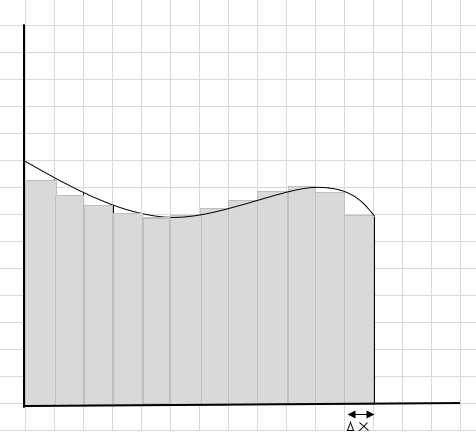
तपाईले देख्न सक्नुहुन्छ कि यी आयतहरू ठूला आयताकार खण्डहरू भन्दा राम्रो घुमाउरो क्षेत्र भित्र फिट हुन्छन्। यो घुमाउरो क्षेत्रलाई साना खण्डहरू/स्लाइसहरूमा विभाजन गर्ने प्रयास गरौं र वक्र मुनिको क्षेत्र निर्धारण गर्ने प्रयास गरौं।
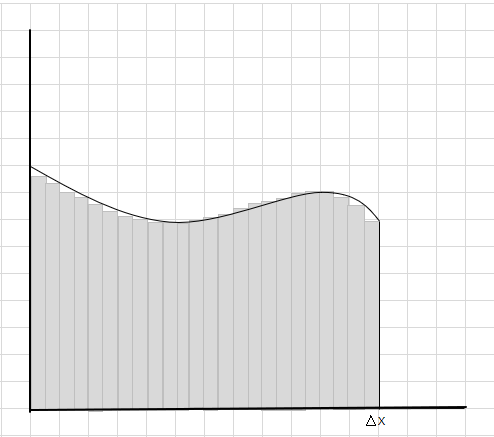
मिस र अतिरिक्त भागहरू बिस्तारै घट्दै छन् र आयतहरू वक्र क्षेत्र भित्र धेरै राम्रो फिट छन्। हामी यी सबै आयतहरूको क्षेत्रफलको योगफलले वक्र मुनिको क्षेत्रफलको राम्रो अनुमान गर्न सक्छौं। वा अर्को शब्दमा, हामी भन्न सक्छौं कि स्लाइसहरू चौडाइमा शून्यमा पुग्दा जवाफ साँचो उत्तरमा पुग्छ। हामी अब \(\Delta x\) को लागि dx लेख्छौं जसको अर्थ चौडाइ शून्यमा आउँदैछ।
यहाँ अभिन्न क्याल्कुलसको लागि सूत्र निकालौं:
मानौं कि हामीले बिन्दु ए र बी बीचको यो वक्र अन्तर्गत क्षेत्र पत्ता लगाउन आवश्यक छ: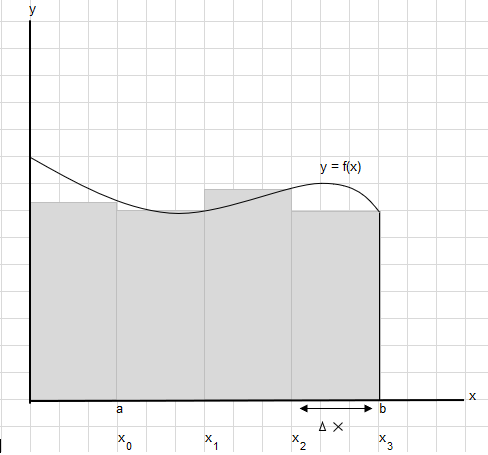
प्रत्येक आयतको चौडाइ \(\Delta x\) हुने गरी a र b बीचको क्षेत्रफललाई बराबर खण्डहरूमा विभाजन गर्नुहोस्।
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
यी आयतहरूको क्षेत्रफलको योगफल \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) रूपमा लेख्न सकिन्छ।
\(\Delta x \) सानो हुँदा वा अन्य शब्दहरूमा खण्डहरूको संख्या बढ्दा हामीले क्षेत्रफलको राम्रो अनुमान गर्न सक्छौं। त्यसैले \(\Delta x \) पातलो र पातलो हुन्छ र n ठूलो र ठूलो हुन्छ। n अनन्ततामा पुग्दा र \(\Delta x \) असीमित रूपमा सानो हुँदै जाँदा हामीले सीमा लिँदा राम्रो सन्निकटन प्राप्त गर्ने यो धारणा इन्टिग्रल हो।
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) x = a र x = b बीचको x को f मुनिको क्षेत्र प्रतिनिधित्व गर्दछ
Integral खोज्नु डेरिभेटिभहरू खोज्नुको उल्टो हो।
x 2 को व्युत्पन्न 2x हो। त्यसैले 2x को एक पूर्णांक x 2 हो।
\(\int 2x \space dx = x^2 + C\) , जहाँ C स्थिर हुन्छ। constant को व्युत्पन्न 0 हुनाले x 2 , x 2 +4, x 2 +10, x 2 +99 को व्युत्पन्न 2x हो। त्यसैले 2x को integral x 2 +C हो।
सामान्य प्रकार्यहरूको अभिन्न अंगहरू हेरौं:
| साझा कार्यहरू | समारोह | अभिन्न |
| स्थिर | \(\int a \cdot dx\) | \(ax + c\) |
| चर | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| वर्ग | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| घातीय | \(\int e^x \cdot dx\) | \(e^x + c\) |
| त्रिकोणमिति(x in radians) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
साझा एकीकरण नियम:
| नियमहरू | समारोह | अभिन्न |
| स्थिर द्वारा गुणन | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| शक्ति नियम (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| योग नियम | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| भिन्नता नियम | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Integrals को कक्षाहरू
\(\int f(x) \space dx\) अनिश्चित अभिन्न प्रतिनिधित्व गर्दछ र \(\int_a^bf(x) \cdot dx\) निश्चित अभिन्न प्रतिनिधित्व गर्दछ। एक निश्चित अभिन्न सुरु र अन्त्य मानहरू छन्। यहाँ a र b लाई सीमा वा सीमा भनिन्छ। अनिश्चित अभिन्न एकीकरण को एक सामान्य रूप को अधिक हो र प्रकार्य को विरोधी व्युत्पन्न को रूप मा व्याख्या गर्न सकिन्छ।
अनिश्चित पूर्णांकलाई a , र b मा, त्यसपछि घटाएर गणना गरेर हामीले Definite Integral पत्ता लगाउँछौं। यसलाई एउटा उदाहरणबाट बुझौं:
हामीलाई थाहा छ \(\int 2x \cdot dx = x^2 + C\) निश्चित पूर्णांकको मूल्य के हुनेछ \(\int _1^2 2x \cdot dx \) ?
x =1 मा, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2 मा, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
घटाउनुहोस् (4 + C) - (1 + C) = 3
को मान \(\int _1^2 2x \cdot dx \) = 3