Je leert:
Integralen samen met afgeleiden zijn de fundamentele objecten in de calculus. Het proces van het berekenen van een integraal wordt integratie genoemd en benaderende berekening van een integraal wordt numerieke integratie genoemd.
Er zijn twee klassen van integralen - bepaalde integralen (zoals 5) en onbepaalde integralen, die onder- en bovengrenzen hebben zoals \(\int_a^bf(x) \cdot dx\) .
Wat is Integraal?
Stel dat we het gebied onder de curve en de bovenstaande x-as moeten vinden.
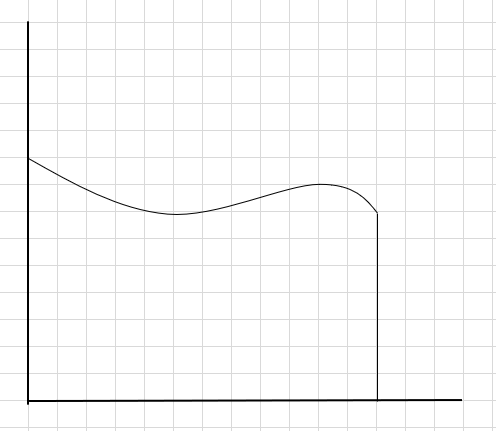
Een manier om dat te doen is om het gebied in vier segmenten te verdelen en vervolgens een rechthoek te tekenen (met behulp van deze segmentlijn) zodat de rechterbovenhoek van elke rechthoek de curve raakt (zoals hieronder weergegeven)
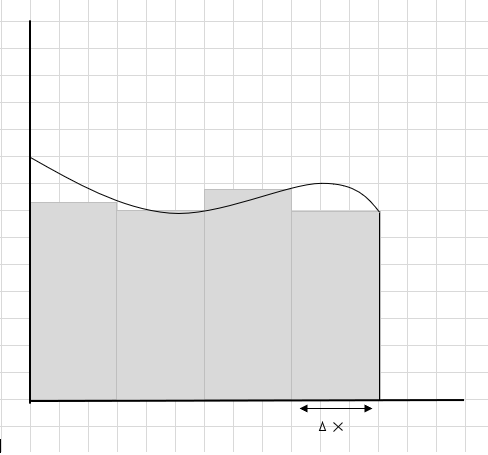
De som van de oppervlakte van deze rechthoekige segmenten is de geschatte oppervlakte onder deze kromme. \(\Delta x \) is de breedte van de rechthoeken/plakjes. Wat vind je van de geschatte oppervlakte?
Een groot deel van de curve wordt gemist en er wordt rekening gehouden met een paar extra onderdelen bij het berekenen van de oppervlakte van dit curvegebied. Check-in onderstaande afbeelding donkergrijs gebied staat voor missen en extra onderdelen.
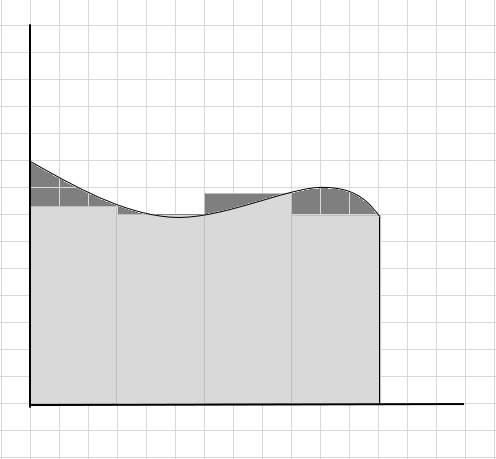
We kunnen zeggen dat dit een slechte schatting is van de oppervlakte van het gebogen gebied, aangezien rechthoeken niet precies onder de curve passen. Laten we het gebied onder deze curve opdelen in kleinere segmenten.
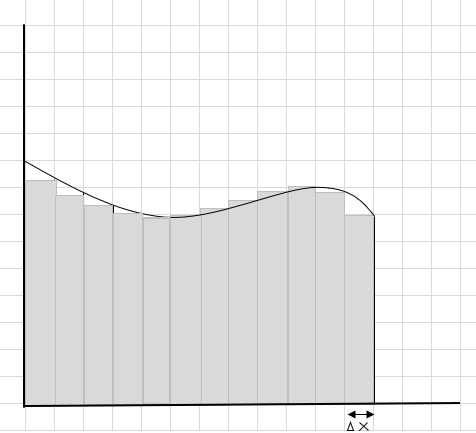
U kunt zien dat deze rechthoeken beter binnen het gebogen gebied passen dan de grotere rechthoekige segmenten. Laten we proberen dit gebogen gebied in kleinere segmenten/plakken te verdelen en proberen het gebied onder de curve te bepalen.
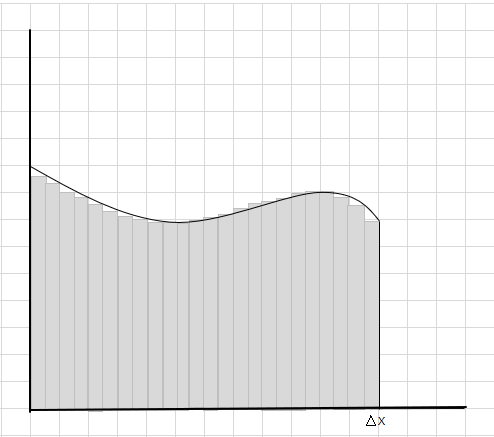
De missers en extra onderdelen worden geleidelijk kleiner en rechthoeken passen veel beter in het curvegebied. We kunnen hieruit afleiden dat de som van de oppervlakte van al deze rechthoeken een goede schatting geeft van de oppervlakte onder de kromme. Of met andere woorden, we kunnen zeggen dat als de segmenten de nul naderen in de breedte, het antwoord het ware antwoord benadert. We schrijven nu dx voor \(\Delta x\) om aan te geven dat de breedte nul nadert.
Laten we hier de formule voor integraalrekening afleiden:
Stel dat we het gebied onder deze curve tussen punt a en b moeten vinden: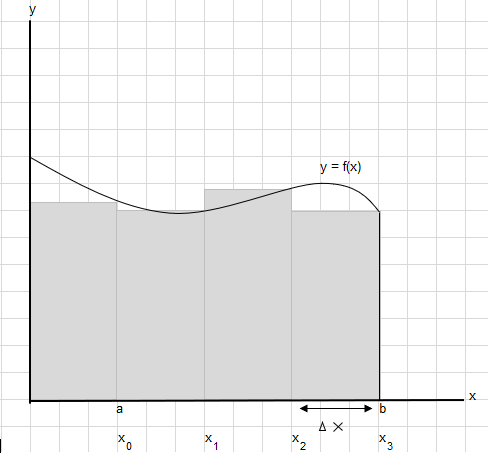
Verdeel het gebied tussen a en b in gelijke segmenten zodat de breedte van elke rechthoek \(\Delta x\) is.
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
De som van de oppervlakte van deze rechthoeken kan worden geschreven als \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
We kunnen de oppervlakte beter benaderen als \(\Delta x \) kleiner wordt of met andere woorden wanneer een aantal segmenten toeneemt. Dus \(\Delta x \) wordt dunner en dunner en n wordt groter en groter. Dit idee van een betere benadering als we de limiet nemen als n oneindig nadert en \(\Delta x \) oneindig klein wordt, is Integraal.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) vertegenwoordigt het gebied onder f van x tussen x = a en x = b
Het vinden van Integraal is het omgekeerde van het vinden van Derivaten.
Afgeleide van x 2 is 2x. Dus een integraal van 2x is x 2 .
\(\int 2x \space dx = x^2 + C\) , waarbij C een constante is. Omdat de afgeleide van constante 0 is, is de afgeleide van x 2 , x 2 +4, x 2 +10, x 2 +99 2x. Daarom is integraal van 2x x 2 +C.
Laten we eens kijken naar integralen van veelvoorkomende functies:
| Algemene functies | Functie | Integraal |
| Constante | \(\int a \cdot dx\) | \(ax + c\) |
| Variabele | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Vierkant | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| exponentieel | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometrie (x in radialen) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Gemeenschappelijke integratieregels:
| Reglement | Functie | Integraal |
| Vermenigvuldiging met constante | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Machtsregel (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Somregel | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Verschil regel | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Klassen van integralen
\(\int f(x) \space dx\) staat voor de onbepaalde integraal en \(\int_a^bf(x) \cdot dx\) staat voor een bepaalde integraal. Een bepaalde integraal heeft begin- en eindwaarden. Hier worden a en b limieten of grenzen genoemd. De onbepaalde integraal is meer een algemene vorm van integratie en kan worden geïnterpreteerd als een anti-afgeleide van de functie.
We vinden de Definitieve Integraal door de onbepaalde Integraal te berekenen bij a , en bij b , en dan af te trekken. Laten we dit aan de hand van een voorbeeld begrijpen:
We kennen \(\int 2x \cdot dx = x^2 + C\) . Wat is de waarde van een bepaalde integraal \(\int _1^2 2x \cdot dx \) ?
Bij x = 1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Bij x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Aftrekken (4 + C) - (1 + C) = 3
Waarde van \(\int _1^2 2x \cdot dx \) = 3