Nauczysz się:
Całki wraz z pochodnymi są podstawowymi obiektami rachunku różniczkowego. Proces obliczania całki nazywa się całkowaniem , a przybliżone obliczenie całki nazywa się całkowaniem numerycznym.
Istnieją dwie klasy całek - całki oznaczone (jak 5) i całki nieoznaczone, które mają dolną i górną granicę jak \(\int_a^bf(x) \cdot dx\) .
Co to jest integralny?
Powiedzmy, że musimy znaleźć pole pod krzywą i powyższą oś x.
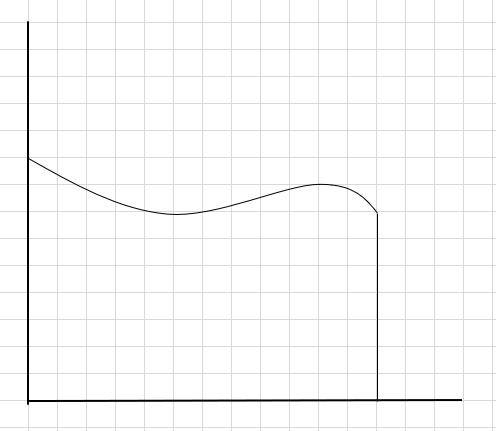
Jednym ze sposobów jest podzielenie regionu na cztery segmenty, a następnie narysowanie prostokąta (za pomocą tej linii segmentu) w taki sposób, aby prawy górny róg każdego prostokąta dotykał krzywej (jak podano poniżej)
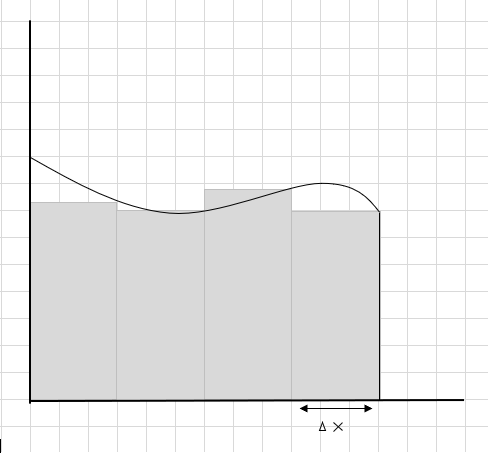
Suma powierzchni tych prostokątnych segmentów jest szacowanym polem pod tą krzywą. \(\Delta x \) jest szerokością prostokątów/plastrów. Co sądzicie o szacowanej powierzchni?
Wiele części krzywej jest pomijanych, a kilka dodatkowych części jest branych pod uwagę podczas obliczania pola tego obszaru krzywej. Zameldowanie poniżej obrazu ciemnoszary region reprezentuje pominięte i dodatkowe części.
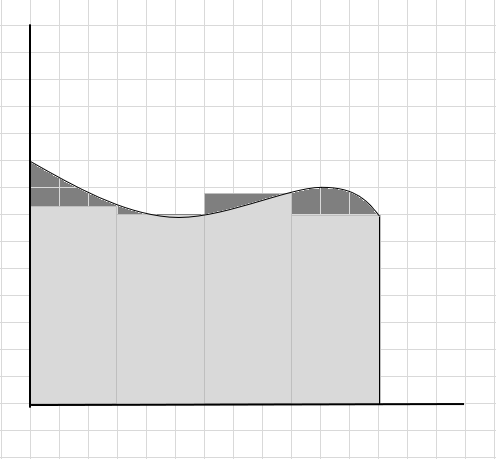
Można powiedzieć, że jest to złe oszacowanie obszaru zakrzywionego obszaru, ponieważ prostokąty nie mieszczą się dokładnie pod krzywą. Podzielmy obszar pod tą krzywą na mniejsze segmenty.
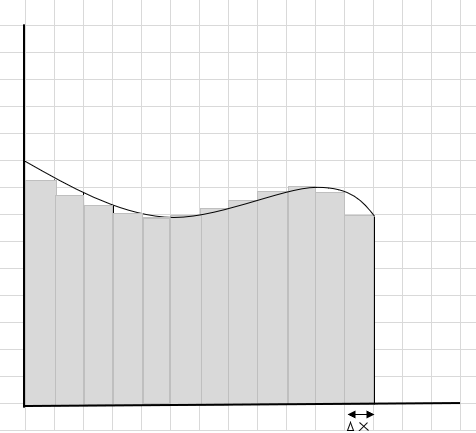
Widać, że te prostokąty lepiej pasują do zakrzywionego obszaru niż większe segmenty prostokątne. Spróbujmy podzielić ten zakrzywiony obszar na mniejsze segmenty/plasterki i spróbujmy określić obszar pod krzywą.
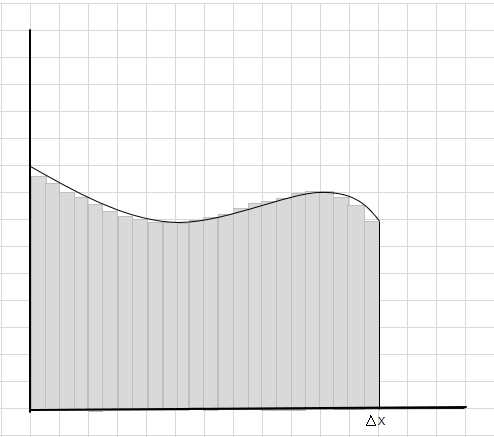
Braki i dodatkowe części stopniowo się zmniejszają, a prostokąty znacznie lepiej pasują do obszaru krzywej. Możemy wywnioskować, że suma pól wszystkich tych prostokątów daje dobre oszacowanie pola pod krzywą. Innymi słowy, możemy powiedzieć, że gdy plasterki zbliżają się do zera, odpowiedź zbliża się do prawdziwej odpowiedzi. Piszemy teraz dx dla \(\Delta x\) to oznacza, że szerokość zbliża się do zera.
Wyprowadźmy tutaj wzór na rachunek całkowy:
Powiedzmy, że musimy znaleźć pole pod tą krzywą między punktami a i b: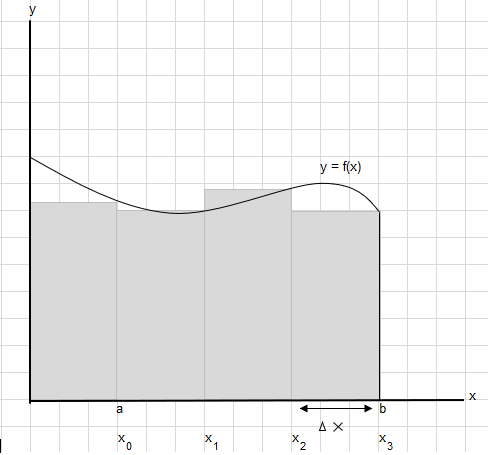
Podziel obszar między a i b na równe segmenty, tak aby szerokość każdego prostokąta wynosiła \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Sumę pól tych prostokątów można zapisać jako \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Możemy mieć lepsze przybliżenie powierzchni, gdy \(\Delta x \) zmniejsza się lub innymi słowy, gdy liczba segmentów wzrasta. Więc \(\Delta x \) staje się cieńszy i cieńszy, a n staje się coraz większy. To pojęcie uzyskania lepszego przybliżenia, gdy przyjmiemy granicę, gdy n dąży do nieskończoności i \(\Delta x \) staje się nieskończenie małe, jest całkowe.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) reprezentuje pole pod f od x między x = a i x = b
Znajdowanie całki jest odwrotnością znajdowania pochodnych.
Pochodna x 2 to 2x. Więc całka z 2x to x 2 .
\(\int 2x \space dx = x^2 + C\) , gdzie C jest stałą. Skoro pochodna stałej wynosi 0, to pochodna x 2 , x 2 +4, x 2 +10, x 2 +99 wynosi 2x. Zatem całka z 2x to x 2 + C.
Spójrzmy na całki wspólnych funkcji:
| Wspólne funkcje | Funkcjonować | Całka |
| Stały | \(\int a \cdot dx\) | \(ax + c\) |
| Zmienny | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Kwadrat | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Wykładniczy | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trygonometria(x w radianach) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Wspólne zasady integracji:
| Zasady | Funkcjonować | Całka |
| Mnożenie przez stałą | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Zasada potęgi (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Reguła sumy | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Reguła różnicy | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Klasy całek
\(\int f(x) \space dx\) reprezentuje całkę nieoznaczoną, a \(\int_a^bf(x) \cdot dx\) reprezentuje całkę oznaczoną. Całka oznaczona ma wartości początkowe i końcowe. Tutaj aib nazywane są granicami lub granicami. Całka nieoznaczona jest bardziej ogólną formą całkowania i może być interpretowana jako funkcja pierwotna funkcji.
Obliczamy Całkę Oznaczoną, obliczając Całkę Nieoznaczoną w a i b , a następnie odejmując. Zrozummy to na przykładzie:
Wiemy \(\int 2x \cdot dx = x^2 + C\) . Jaka będzie wartość całki oznaczonej \(\int _1^2 2x \cdot dx \) ?
Przy x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Przy x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Odejmij (4 + C) - (1 + C) = 3
Wartość \(\int _1^2 2x \cdot dx \) = 3