Você vai aprender:
Integrais junto com derivadas são os objetos fundamentais do cálculo. O processo de cálculo de uma integral é chamado de integração e o cálculo aproximado de uma integral é denominado integração numérica.
Existem duas classes de integrais - integral definida (como 5) e integrais indefinidas, que tem limites inferior e superior como \(\int_a^bf(x) \cdot dx\) .
O que é Integral?
Digamos que temos que encontrar a área sob a curva e o eixo x acima.
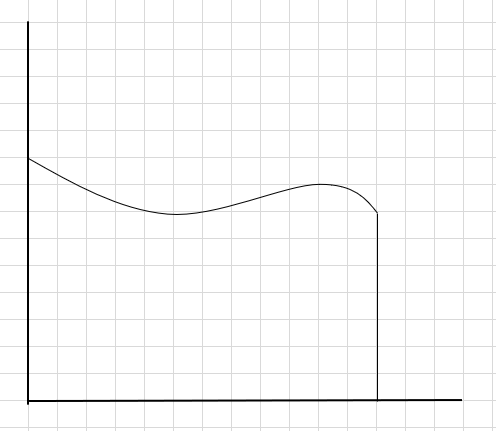
Uma maneira de fazer é dividir a região em quatro segmentos e, em seguida, desenhar um retângulo (usando esta linha de segmento) de modo que o canto superior direito de cada retângulo toque a curva (conforme dado abaixo)
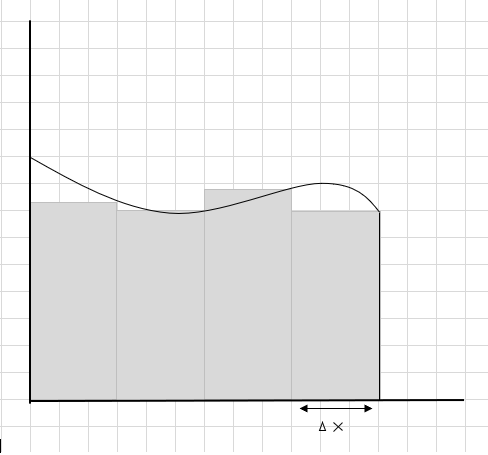
A soma da área desses segmentos retangulares é a área estimada sob esta curva. \(\Delta x \) sendo a largura dos retângulos/fatias. O que você acha da área estimada?
Muitas partes da curva são perdidas e algumas partes adicionais são consideradas ao calcular a área dessa região da curva. O check-in abaixo da região cinza escuro da imagem representa peças perdidas e adicionais.
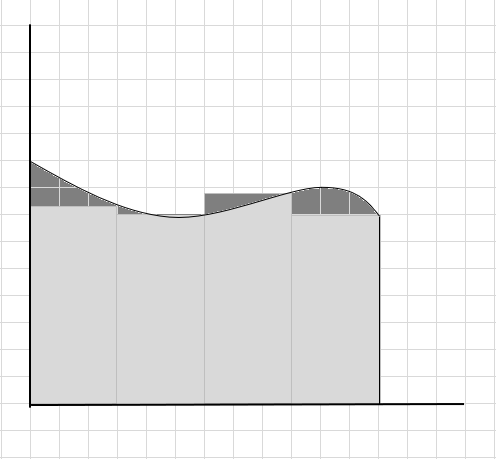
Podemos dizer que esta é uma estimativa ruim da área da região curva, pois os retângulos não se encaixam exatamente sob a curva. Vamos dividir a área sob esta curva em segmentos menores.
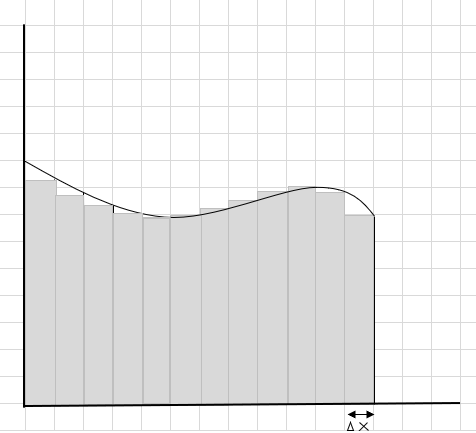
Você pode ver que esses retângulos se encaixam melhor dentro da área curva do que os segmentos retangulares maiores. Vamos tentar dividir esta região curva em segmentos/fatias menores e tentar determinar a área sob a curva.
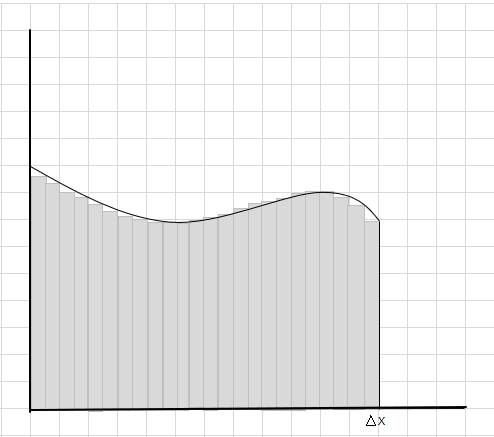
As peças perdidas e extras estão diminuindo gradualmente e os retângulos estão se encaixando muito melhor dentro da região da curva. Podemos inferir que a soma da área de todos esses retângulos fornece uma boa estimativa da área sob a curva. Ou em outras palavras, podemos dizer que à medida que as fatias se aproximam de zero em largura, a resposta se aproxima da resposta verdadeira. Agora escrevemos dx para \(\Delta x\) para significar que a largura está se aproximando de zero.
Vamos derivar a fórmula para o cálculo integral aqui:
Digamos que precisamos encontrar a área sob esta curva entre os pontos a e b: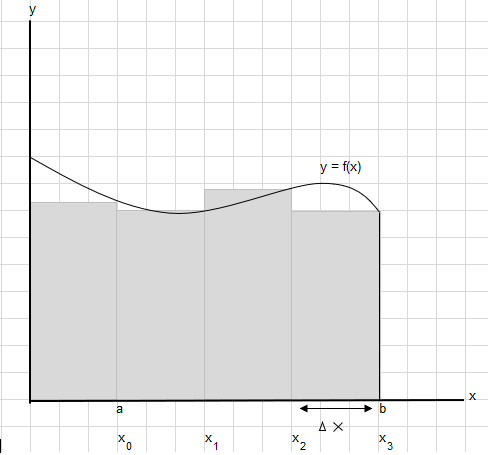
Divida a área entre a e b em segmentos iguais de modo que a largura de cada retângulo seja \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
A soma da área desses retângulos pode ser escrita como \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Podemos ter uma melhor aproximação da área à medida que \(\Delta x \) diminui ou em outras palavras quando aumenta o número de segmentos. Então \(\Delta x \) fica cada vez mais fino e n fica cada vez maior. Esta noção de obter uma melhor aproximação à medida que tomamos o limite quando n se aproxima do infinito e \(\Delta x \) tornando-se infinitesimalmente pequeno é Integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) representa a área sob f de x entre x = a e x = b
Encontrar integral é o inverso de encontrar derivadas.
A derivada de x 2 é 2x. Então uma integral de 2x é x 2 .
\(\int 2x \space dx = x^2 + C\) , onde C é uma constante. Como a derivada da constante é 0, portanto, a derivada de x 2 , x 2 +4, x 2 +10, x 2 +99 é 2x. Portanto integral de 2x é x 2 +C.
Vejamos as integrais de funções comuns:
| Funções comuns | Função | Integrante |
| Constante | \(\int a \cdot dx\) | \(ax + c\) |
| Variável | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Quadrado | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Exponencial | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometria (x em radianos) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Regras comuns de integração:
| Regras | Função | Integrante |
| Multiplicação por constante | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Regra de Potência(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Regra de soma | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Regra de diferença | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Classes de integrais
\(\int f(x) \space dx\) representa a integral indefinida e \(\int_a^bf(x) \cdot dx\) representa uma integral definida. Uma integral definida tem valores iniciais e finais. Aqui a e b são chamados limites ou fronteiras. A integral indefinida é mais uma forma geral de integração e pode ser interpretada como antiderivada da função.
Encontramos a Integral Definida calculando a Integral indefinida em a , e em b , depois subtraindo. Vamos entender isso com um exemplo:
Sabemos que \(\int 2x \cdot dx = x^2 + C\) . Qual será o valor de uma integral definida \(\int _1^2 2x \cdot dx \) ?
Em x = 1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Em x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Subtrair (4 + C) - (1 + C) = 3
Valor de \(\int _1^2 2x \cdot dx \) = 3