Ты выучишь:
Интегралы вместе с производными являются фундаментальными объектами исчисления. Процесс вычисления интеграла называется интегрированием , а приближенное вычисление интеграла называется численным интегрированием.
Есть два класса интегралов - определенный интеграл (например, 5) и неопределенный интеграл, который имеет нижний и верхний пределы, такие как \(\int_a^bf(x) \cdot dx\) .
Что такое Интеграл?
Допустим, нам нужно найти площадь под кривой и указанной выше оси x.
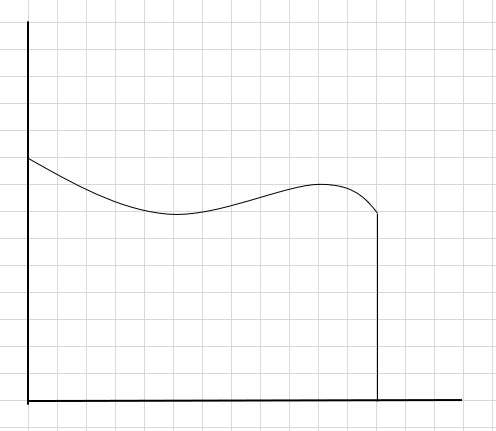
Один из способов сделать это — разделить область на четыре сегмента, а затем нарисовать прямоугольник (используя эту линию сегмента) так, чтобы верхний правый угол каждого прямоугольника касался кривой (как показано ниже).
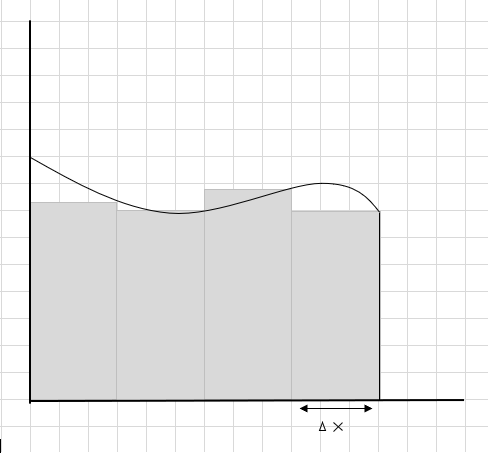
Сумма площадей этих прямоугольных сегментов является расчетной площадью под этой кривой. \(\Delta x \) - ширина прямоугольников/срезов. Что вы думаете о предполагаемой площади?
Большая часть кривой пропущена, и несколько дополнительных частей учитываются при расчете площади этой области кривой. Темно-серая область на изображении внизу представляет недостающие и дополнительные части.
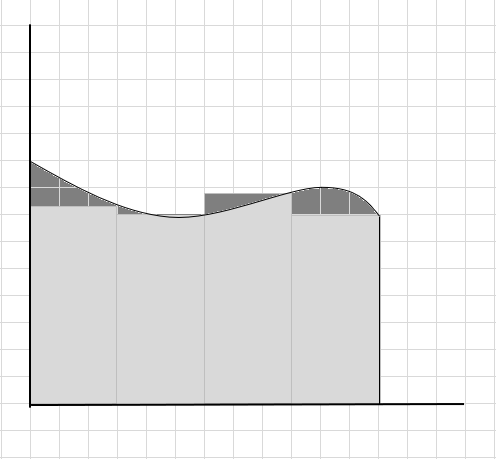
Мы можем сказать, что это плохая оценка площади искривленной области, поскольку прямоугольники не точно подходят под кривую. Разделим площадь под этой кривой на более мелкие отрезки.
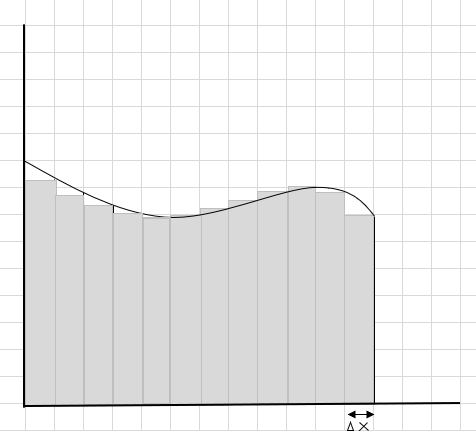
Вы можете видеть, что эти прямоугольники вписываются в изогнутую область лучше, чем большие прямоугольные сегменты. Давайте попробуем разделить эту изогнутую область на более мелкие сегменты/срезы и попробуем определить площадь под кривой.
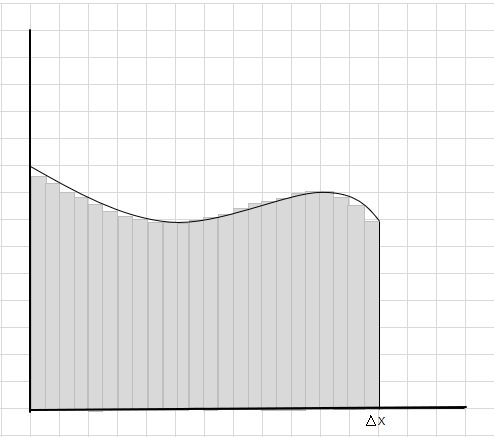
Промахи и лишние части постепенно уменьшаются, и прямоугольники намного лучше вписываются в область кривой. Мы можем сделать вывод, что сумма площадей всех этих прямоугольников дает хорошую оценку площади под кривой. Или, другими словами, мы можем сказать, что по мере того, как срезы приближаются к нулю по ширине, ответ приближается к истинному ответу. Теперь мы пишем dx вместо \(\Delta x\) , что означает, что ширина приближается к нулю.
Выведем здесь формулу интегрального исчисления:
Допустим, нам нужно найти площадь под этой кривой между точками a и b: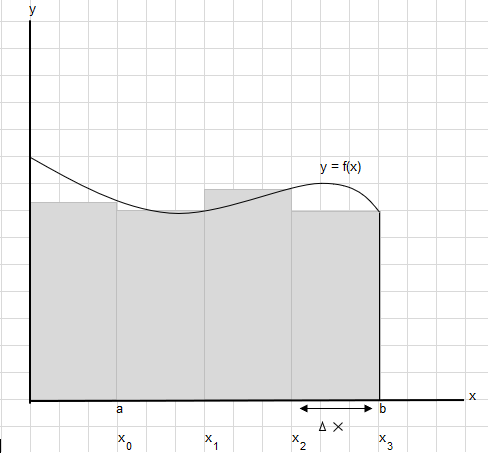
Разделите площадь между a и b на равные сегменты так, чтобы ширина каждого прямоугольника была \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Сумма площадей этих прямоугольников может быть записана как \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
У нас может быть лучшее приближение площади, когда \(\Delta x \) становится меньше или, другими словами, когда количество сегментов увеличивается. Таким образом, \(\Delta x \) становится все тоньше и тоньше, а n становится все больше и больше. Это понятие улучшения приближения по мере того, как мы берем предел, когда n приближается к бесконечности, а \(\Delta x \) становится бесконечно малым, является интегралом.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) представляет площадь под f числа x между x = a и x = b
Нахождение интеграла — это процесс, обратный нахождению производных.
Производная х 2 равна 2х. Таким образом, интеграл от 2x равен x 2 .
\(\int 2x \space dx = x^2 + C\) , где C — константа. Поскольку производная константы равна 0, следовательно, производная от x 2 , x 2 +4, x 2 +10, x 2 +99 равна 2x. Следовательно, интеграл от 2x равен x 2 +C.
Давайте посмотрим на интегралы общих функций:
| Общие функции | Функция | интеграл |
| Постоянный | \(\int a \cdot dx\) | \(ax + c\) |
| Переменная | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Площадь | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| экспоненциальный | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Тригонометрия (x в радианах) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Общие правила интеграции:
| Правила | Функция | интеграл |
| Умножение на константу | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Правило силы (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Правило суммы | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Правило разницы | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Классы интегралов
\(\int f(x) \space dx\) представляет собой неопределенный интеграл, а \(\int_a^bf(x) \cdot dx\) представляет собой определенный интеграл. Определенный интеграл имеет начальное и конечное значения. Здесь a и b называются пределами или границами. Неопределенный интеграл является более общей формой интегрирования и может быть интерпретирован как антипроизводная функции.
Мы находим определенный интеграл, вычисляя неопределенный интеграл в точках a и b , а затем вычитая. Разберем это на примере:
Мы знаем \(\int 2x \cdot dx = x^2 + C\) . Каким будет значение определенного интеграла \(\int _1^2 2x \cdot dx \) ?
При x = 1 \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
При x = 2 \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Вычесть (4 + С) - (1 + С) = 3
Значение \(\int _1^2 2x \cdot dx \) = 3