Ti do të mësosh:
Integralet së bashku me derivatet janë objektet themelore në llogaritje. Procesi i llogaritjes së një integrali quhet integrim dhe llogaritja e përafërt e një integrali quhet integrim numerik.
Ekzistojnë dy klasa integralesh - integral i caktuar (si 5) dhe integral i pacaktuar, i cili ka kufij të poshtëm dhe të sipërm si \(\int_a^bf(x) \cdot dx\) .
Çfarë është Integrale?
Le të themi se duhet të gjejmë zonën nën kurbë dhe boshtin e mësipërm x.
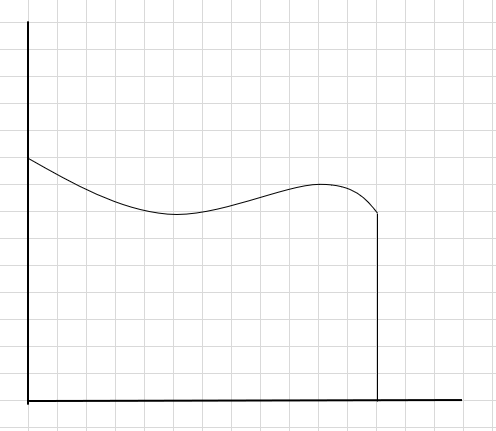
Një mënyrë për të bërë është të ndani rajonin në katër segmente dhe më pas të vizatoni një drejtkëndësh (duke përdorur këtë vijë segmenti) në mënyrë që këndi i sipërm i djathtë i çdo drejtkëndëshi të prekë kurbën (siç jepet më poshtë)
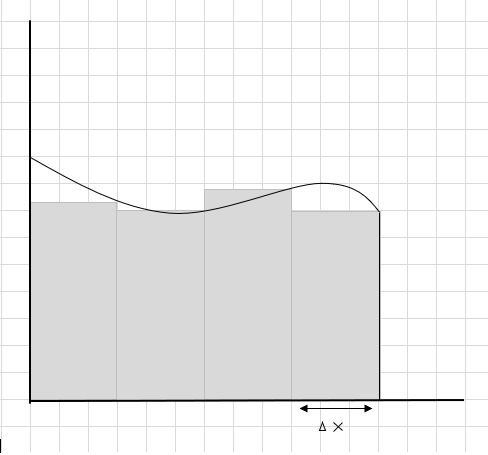
Shuma e sipërfaqes së këtyre segmenteve drejtkëndëshe është sipërfaqja e vlerësuar nën këtë kurbë. \(\Delta x \) është gjerësia e drejtkëndëshave/fetave. Çfarë mendoni për sipërfaqen e vlerësuar?
Një pjesë e madhe e kurbës mungon dhe disa pjesë shtesë merren parasysh gjatë llogaritjes së sipërfaqes së këtij rajoni kurbë. Regjistrimi poshtë imazhit, zona gri e errët përfaqëson mungesën dhe pjesët shtesë.
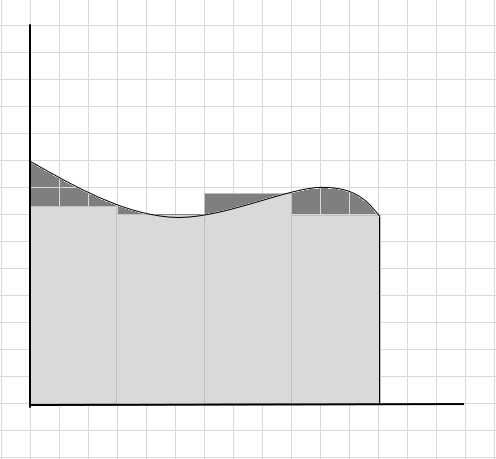
Mund të themi se ky është një vlerësim i dobët i sipërfaqes së rajonit të lakuar pasi drejtkëndëshat nuk përshtaten saktësisht nën kurbë. Le ta ndajmë zonën nën këtë kurbë në segmente më të vogla.
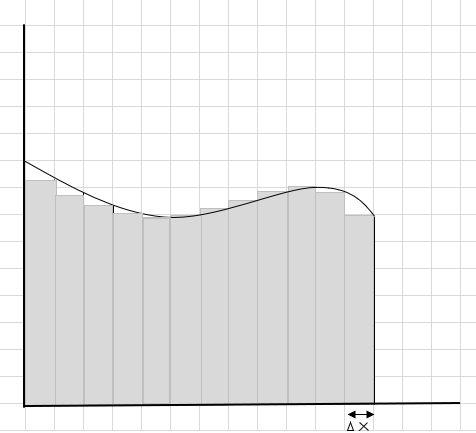
Ju mund të shihni se këto drejtkëndësha përshtaten brenda zonës së lakuar më mirë se segmentet më të mëdha drejtkëndëshe. Le të përpiqemi ta ndajmë këtë rajon të lakuar në segmente/feta më të vogla dhe të përpiqemi të përcaktojmë zonën nën kurbë.
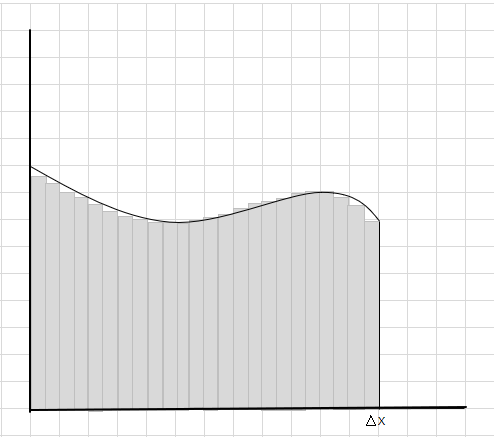
Mungesa dhe pjesët shtesë po zvogëlohen gradualisht dhe drejtkëndëshat po përshtaten shumë më mirë brenda rajonit të kurbës. Mund të konkludojmë se shuma e sipërfaqes së të gjithë këtyre drejtkëndëshave jep një vlerësim të mirë të zonës nën kurbë. Ose me fjalë të tjera, mund të themi kur fetat i afrohen zeros në gjerësi, përgjigja i afrohet përgjigjes së vërtetë. Tani shkruajmë dx për \(\Delta x\) të do të thotë që gjerësia po i afrohet zeros.
Le të nxjerrim formulën për llogaritjen integrale këtu:
Le të themi se duhet të gjejmë zonën nën këtë kurbë midis pikës a dhe b: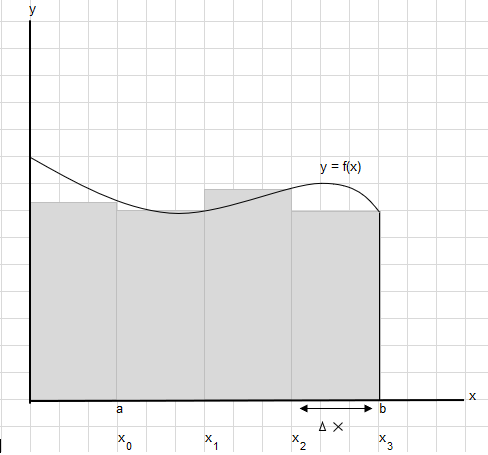
Ndani zonën midis a dhe b në segmente të barabarta në mënyrë që gjerësia e çdo drejtkëndëshi të jetë \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Shuma e sipërfaqes së këtyre drejtkëndëshave mund të shkruhet si \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Mund të kemi një përafrim më të mirë të zonës kur \(\Delta x \) bëhet më e vogël ose me fjalë të tjera kur një numër segmentesh rritet. Pra, \(\Delta x \) bëhet më e hollë dhe më e hollë dhe n bëhet gjithnjë e më e madhe. Ky nocion i arritjes së përafrimit më të mirë ndërsa marrim kufirin kur n i afrohet pafundësisë dhe \(\Delta x \) duke u bërë pafundësisht i vogël është integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) përfaqëson zonën nën f të x midis x = a dhe x = b
Gjetja e integralit është e kundërta e gjetjes së derivateve.
Derivati i x 2 është 2x. Pra, një integral i 2x është x 2 .
\(\int 2x \space dx = x^2 + C\) , ku C është një konstante. Duke qenë se derivati i konstantës është 0, pra derivati i x 2 , x 2 +4, x 2 +10, x 2 +99 është 2x. Prandaj integrali i 2x është x 2 +C.
Le të shohim integralet e funksioneve të zakonshme:
| Funksionet e Përbashkëta | Funksioni | Integrale |
| Konstante | \(\int a \cdot dx\) | \(ax + c\) |
| E ndryshueshme | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Sheshi | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Eksponenciale | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometria (x në radian) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Rregullat e përbashkëta të integrimit:
| Rregullat | Funksioni | Integrale |
| Shumëzimi me konstante | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Rregulli i fuqisë (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Rregulli i shumës | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Rregulli i ndryshimit | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Klasat e integraleve
\(\int f(x) \space dx\) përfaqëson integralin e pacaktuar dhe \(\int_a^bf(x) \cdot dx\) përfaqëson një integral të caktuar. Një integral i caktuar ka vlera fillestare dhe fundore. Këtu a dhe b quhen kufij ose kufij. Integrali i pacaktuar është më shumë një formë e përgjithshme e integrimit dhe mund të interpretohet si anti-derivat i funksionit.
Integralin e caktuar e gjejmë duke llogaritur integralin e pacaktuar në a , dhe në b , pastaj duke zbritur. Le ta kuptojmë këtë me një shembull:
Ne e dimë \(\int 2x \cdot dx = x^2 + C\) . Sa do të jetë vlera e një integrali të caktuar \(\int _1^2 2x \cdot dx \) ?
Në x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Në x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Zbrit (4 + C) - (1 + C) = 3
Vlera e \(\int _1^2 2x \cdot dx \) = 3