Du kommer att lära dig:
Integraler tillsammans med derivator är de fundamentala objekten i kalkylen. Processen att beräkna en integral kallas integration och ungefärlig beräkning av en integral kallas numerisk integration.
Det finns två klasser av integraler - bestämd integral (som 5) och obestämd integral, som har undre och övre gränser som \(\int_a^bf(x) \cdot dx\)
Vad är Integral?
Låt säga att vi måste hitta arean under kurvan och ovanstående x-axel.
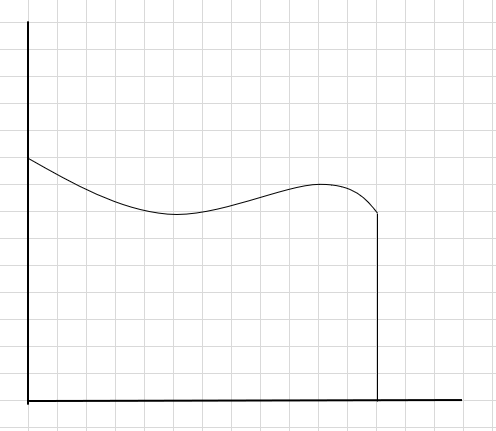
Ett sätt att göra är att dela upp området i fyra segment och sedan rita en rektangel (med denna segmentlinje) så att det övre högra hörnet av varje rektangel vidrör kurvan (enligt nedan)
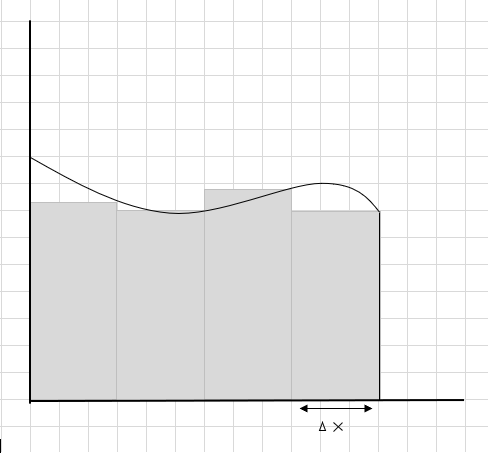
Summan av arean av dessa rektangulära segment är den uppskattade arean under denna kurva. \(\Delta x \) är bredden på rektanglarna/skivorna. Vad tycker du om den beräknade ytan?
En hel del av kurvdelen missas och några ytterligare delar beaktas vid beräkning av arean för denna kurvregion. Incheckning under bilden mörkgrå region representerar miss-out och ytterligare delar.
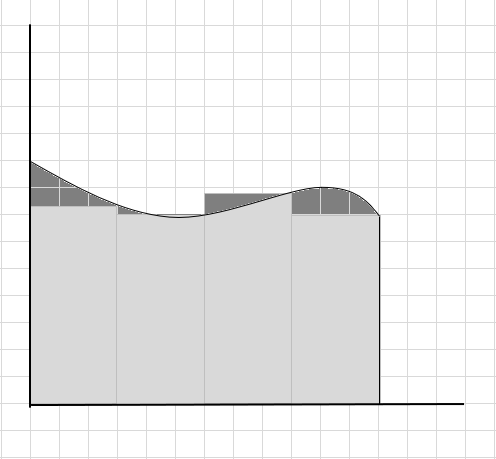
Vi kan säga att detta är en dålig uppskattning av arean av det krökta området eftersom rektanglar inte exakt passar under kurvan. Låt oss dela upp området under denna kurva i mindre segment.
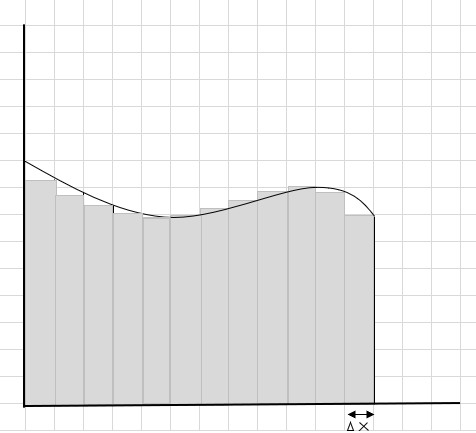
Du kan se att dessa rektanglar passar bättre in i det krökta området än de större rektangulära segmenten. Låt oss försöka dela upp detta krökta område i mindre segment/skivor och försöka bestämma området under kurvan.
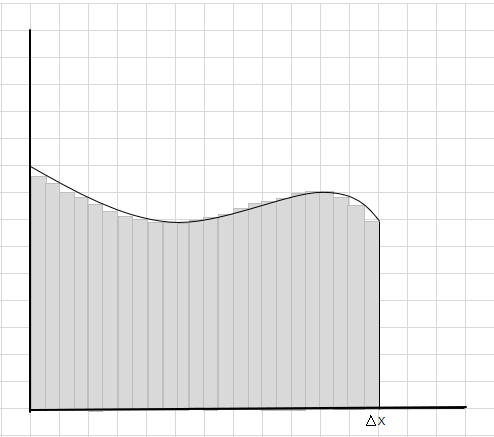
Missen och extradelarna minskar gradvis och rektanglar passar mycket bättre in i kurvområdet. Vi kan dra slutsatsen att summan av arean av alla dessa rektanglar ger en bra uppskattning av arean under kurvan. Eller med andra ord, vi kan säga att när skivorna närmar sig noll i bredd närmar sig svaret det sanna svaret. Vi skriver nu dx för \(\Delta x\) till betyder att bredden närmar sig noll.
Låt oss härleda formeln för integralkalkyl:
Låt säga att vi måste hitta arean under denna kurva mellan punkt a och b: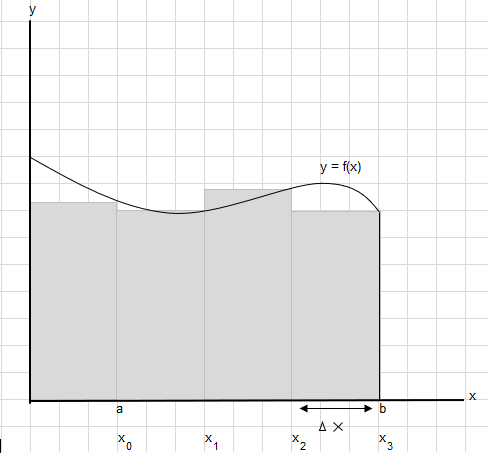
Dela upp området mellan a och b i lika stora segment så att bredden på varje rektangel är \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Summan av arean av dessa rektanglar kan skrivas som \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\)
Vi kan få en bättre approximation av arean när \(\Delta x \) blir mindre eller med andra ord när ett antal segment ökar. Så \(\Delta x \) blir tunnare och tunnare och n blir större och större. Denna föreställning om att få bättre approximation när vi tar gränsen när n närmar sig oändligheten och \(\Delta x \) blir oändligt liten är Integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) representerar arean under f av x mellan x = a och x = b
Att hitta integral är en motsats till att hitta derivat.
Derivat av x 2 är 2x. Så en integral av 2x är x 2 .
\(\int 2x \space dx = x^2 + C\) där C är en konstant. Eftersom derivatan av konstanten är 0, är därför derivatan av x 2 , x 2 +4, x 2 +10, x 2 +99 2x. Därför är integralen av 2x x 2 +C.
Låt oss titta på integraler av vanliga funktioner:
| Vanliga funktioner | Fungera | Väsentlig |
| Konstant | \(\int a \cdot dx\) | \(ax + c\) |
| Variabel | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Fyrkant | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Exponentiell | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometri (x i radianer) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Vanliga integrationsregler:
| Regler | Fungera | Väsentlig |
| Multiplikation med konstant | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Maktregel(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Summaregel | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Skillnadsregel | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Klasser av integraler
\(\int f(x) \space dx\) representerar den obestämda integralen och \(\int_a^bf(x) \cdot dx\) representerar en bestämd integral. En bestämd integral har start- och slutvärden. Här kallas a och b gränser eller gränser. Den obestämda integralen är mer en generell form av integration och kan tolkas som en anti-derivata av funktionen.
Vi hittar den bestämda integralen genom att beräkna den obestämda integralen vid a , och vid b , och sedan subtrahera. Låt oss förstå detta med ett exempel:
Vi vet \(\int 2x \cdot dx = x^2 + C\) . Vad blir värdet av en bestämd integral \(\int _1^2 2x \cdot dx \)
Vid x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Vid x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Subtrahera (4 + C) - (1 + C) = 3
Värdet på \(\int _1^2 2x \cdot dx \) = 3