Utajifunza:
Viunganishi pamoja na viasili ni vitu vya msingi katika kalkulasi. Mchakato wa kukokotoa muunganisho unaitwa muunganisho na makadirio ya hesabu ya kiunganishi huitwa muunganisho wa nambari.
Kuna aina mbili za viambatanisho - viambajengo dhahiri (kama 5) na viunga visivyo na kikomo, ambavyo vina mipaka ya chini na ya juu kama \(\int_a^bf(x) \cdot dx\) .
Integral ni nini?
Wacha tuseme lazima tupate eneo chini ya curve na mhimili wa x hapo juu.
Njia moja ya kufanya ni kugawanya mkoa katika sehemu nne na kisha kuchora mstatili (kwa kutumia mstari wa sehemu hii) ili kona ya juu ya kulia ya kila mstatili inagusa curve (kama ilivyoonyeshwa hapa chini)
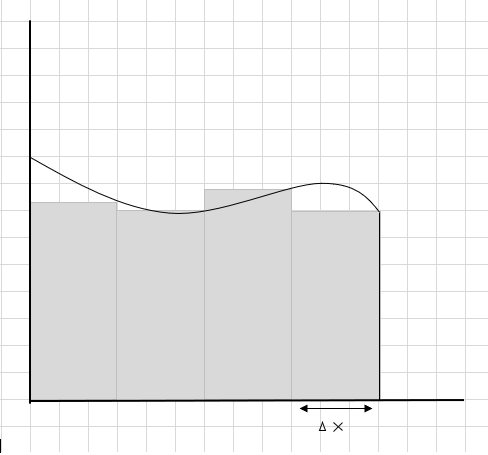
Jumla ya eneo la sehemu hizi za mstatili ni eneo linalokadiriwa chini ya curve hii. \(\Delta x \) kuwa upana wa mistatili/vipande. Una maoni gani kuhusu eneo linalokadiriwa?
Sehemu nyingi za curve hukosa na sehemu chache za ziada huzingatiwa wakati wa kuhesabu eneo la eneo hili la curve. Ingia chini ya picha eneo la kijivu giza linawakilisha kukosa na sehemu za ziada.
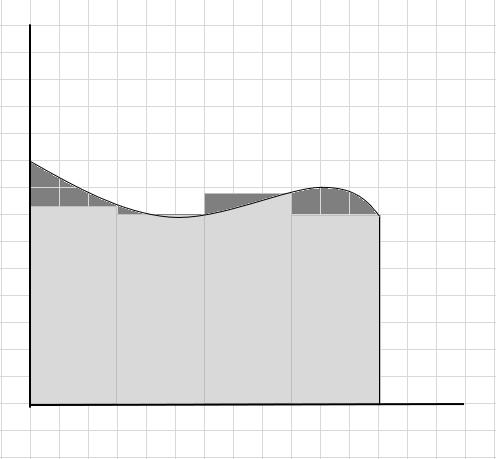
Tunaweza kusema hili ni makadirio duni ya eneo la eneo lililojipinda kwani mistatili haifai kabisa chini ya mkunjo. Wacha tugawanye eneo chini ya curve hii katika sehemu ndogo.
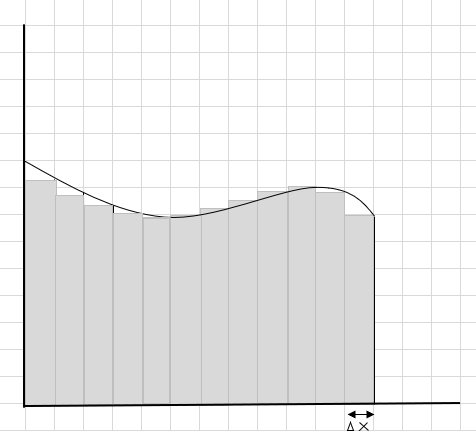
Unaweza kuona kwamba mistatili hii inafaa ndani ya eneo lililojipinda vyema kuliko sehemu kubwa za mstatili. Wacha tujaribu kugawa eneo hili lililojipinda katika sehemu/vipande vidogo na tujaribu kubainisha eneo lililo chini ya curve.
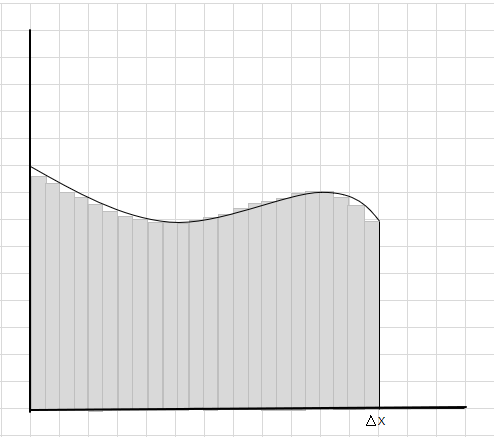
Sehemu zinazokosekana na za ziada zinapungua polepole na mistatili inafaa zaidi ndani ya eneo la curve. Tunaweza kukisia kuwa jumla ya eneo la mistatili hii yote inatoa makadirio mazuri ya eneo lililo chini ya ukingo. Au kwa maneno mengine, tunaweza kusema vipande vinapokaribia sifuri kwa upana jibu linakaribia jibu la kweli. Sasa tunaandika dx kwa \(\Delta x\) kumaanisha kuwa upana unakaribia sufuri.
Wacha tupate formula ya hesabu muhimu hapa:
Wacha tuseme tunahitaji kupata eneo chini ya curve hii kati ya nukta a na b: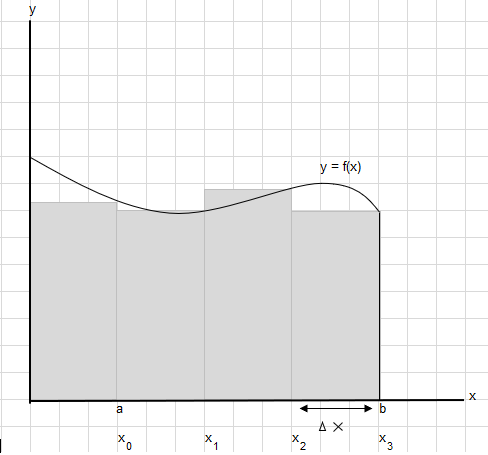
Gawanya eneo kati ya a na b katika sehemu sawa hivi kwamba upana wa kila mstatili ni \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Jumla ya eneo la mistatili hii inaweza kuandikwa kama \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Tunaweza kuwa na ukadiriaji bora wa eneo kadiri \(\Delta x \) inavyopungua au kwa maneno mengine idadi ya sehemu inapoongezeka. Kwa hivyo \(\Delta x \) inakuwa nyembamba na nyembamba na n inakuwa kubwa na kubwa. Wazo hili la kupata ukadiriaji bora tunapochukua kikomo n inapokaribia infinity na \(\Delta x \) kuwa ndogo sana ni Integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) inawakilisha eneo chini ya f ya x kati ya x = a na x = b
Kupata Integral ni kinyume cha kutafuta Mizizi.
Nyingi ya x 2 ni 2x. Kwa hivyo kiungo cha 2x ni x 2 .
\(\int 2x \space dx = x^2 + C\) , ambapo C ni ya kudumu. Kama derivative ya constant ni 0 kwa hivyo derivative ya x 2 , x 2 +4, x 2 +10, x 2 +99 ni 2x. Kwa hivyo muhimu ya 2x ni x 2 +C.
Wacha tuangalie viunga vya kazi za kawaida:
| Kazi za Kawaida | Kazi | Muhimu |
| Mara kwa mara | \(\int a \cdot dx\) | \(ax + c\) |
| Inaweza kubadilika | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Mraba | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Kielelezo | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometry (x katika radiani) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Sheria za kawaida za ujumuishaji:
| Kanuni | Kazi | Muhimu |
| Kuzidisha kwa mara kwa mara | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Kanuni ya Nguvu (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Kanuni ya Jumla | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Kanuni ya Tofauti | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Madarasa ya Viunganishi
\(\int f(x) \space dx\) inawakilisha kiunganishi kisichojulikana na \(\int_a^bf(x) \cdot dx\) inawakilisha kiunganishi dhahiri. Kiunganishi dhahiri kina maadili ya kuanza na mwisho. Hapa a na b inaitwa mipaka au mipaka. Kiunga kisicho na kikomo ni zaidi ya aina ya jumla ya ujumuishaji na inaweza kufasiriwa kama kipingamizi cha chaguo la kukokotoa.
Tunapata Muunganisho Halisi kwa kukokotoa Uunganisho usiojulikana kwa a , na kwa b , kisha kutoa. Hebu tuelewe hili kwa mfano:
Tunajua \(\int 2x \cdot dx = x^2 + C\) . Nini itakuwa thamani ya kiunganishi dhahiri \(\int _1^2 2x \cdot dx \) ?
Kwa x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Kwa x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Ondoa (4 + C) - (1 + C) = 3
Thamani ya \(\int _1^2 2x \cdot dx \) = 3