คุณจะได้เรียนรู้:
ปริพันธ์ และ อนุพันธ์ เป็นวัตถุพื้นฐานใน แคลคูลัส กระบวนการคำนวณอินทิกรัลเรียกว่า อินทิกรัล และการคำนวณโดยประมาณของอินทิกรัลเรียกว่าอินทิกรัลเชิงตัวเลข
ปริพันธ์มี 2 คลาส - อินทิกรัลแน่นอน (เช่น 5) และอินทิกรัลไม่จำกัด ซึ่งมีขีดจำกัดล่างและบนเช่น \(\int_a^bf(x) \cdot dx\)
อินทิกรัลคืออะไร?
สมมติว่าเราต้องหาพื้นที่ใต้เส้นโค้งและแกน x ด้านบน
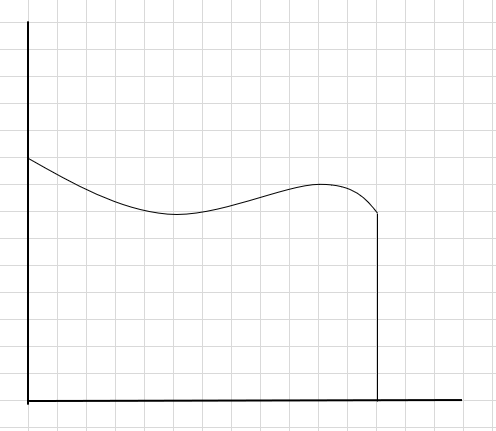
วิธีหนึ่งที่จะทำคือแบ่งพื้นที่ออกเป็นสี่ส่วนแล้ววาดรูปสี่เหลี่ยมผืนผ้า (โดยใช้เส้นแบ่งส่วนนี้) เพื่อให้มุมขวาบนของสี่เหลี่ยมแต่ละอันสัมผัสกับเส้นโค้ง (ตามที่ระบุด้านล่าง)
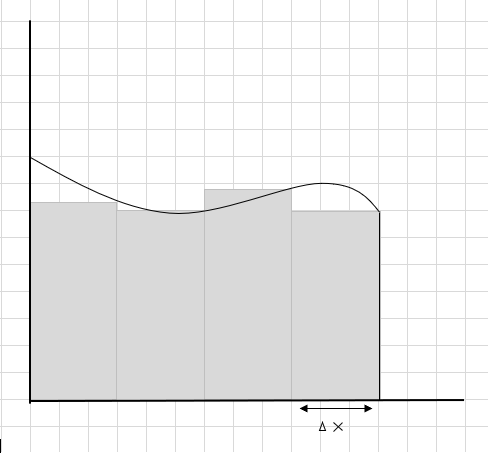
ผลรวมของพื้นที่ของส่วนสี่เหลี่ยมผืนผ้าเหล่านี้คือพื้นที่โดยประมาณภายใต้เส้นโค้งนี้ \(\Delta x \) เป็นความกว้างของสี่เหลี่ยม/ชิ้น คุณคิดอย่างไรเกี่ยวกับพื้นที่โดยประมาณ?
พลาดส่วนของเส้นโค้งไปมากและมีการพิจารณาส่วนเพิ่มเติมอีกสองสามส่วนในขณะที่คำนวณพื้นที่ของส่วนโค้งนี้ การเช็คอินด้านล่างภาพ พื้นที่สีเทาเข้มแสดงถึงส่วนที่พลาดและส่วนเพิ่มเติม
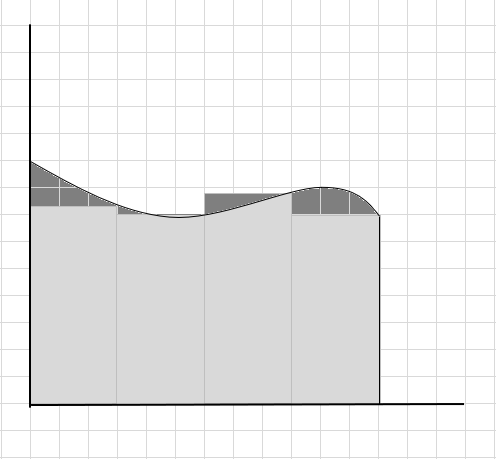
เราสามารถพูดได้ว่านี่เป็นการประมาณพื้นที่ของส่วนโค้งที่แย่เนื่องจากรูปสี่เหลี่ยมผืนผ้าไม่พอดีกับส่วนโค้ง ลองแบ่งพื้นที่ใต้เส้นโค้งนี้ออกเป็นส่วนย่อยๆ
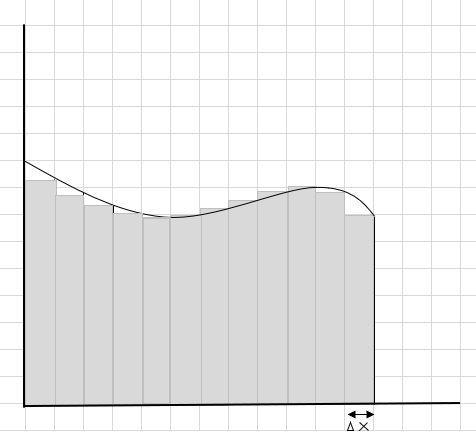
คุณจะเห็นว่าสี่เหลี่ยมเหล่านี้พอดีกับพื้นที่โค้งได้ดีกว่าส่วนที่เป็นสี่เหลี่ยมขนาดใหญ่ มาลองแบ่งพื้นที่โค้งนี้ออกเป็นส่วนย่อย/ส่วนย่อยๆ แล้วลองกำหนดพื้นที่ใต้เส้นโค้งดู
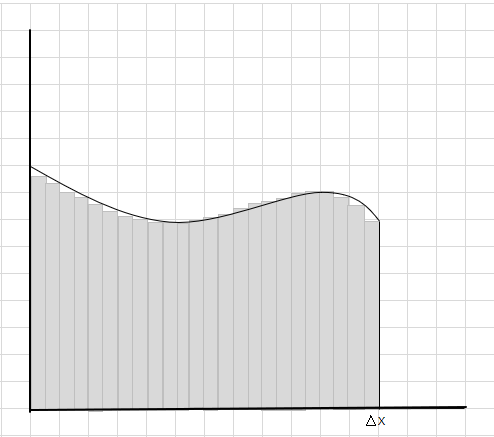
ส่วนพลาดและส่วนพิเศษจะค่อยๆ ลดลง และรูปสี่เหลี่ยมผืนผ้าจะเหมาะสมกว่ามากภายในส่วนโค้ง เราสามารถอนุมานได้ว่าผลรวมของพื้นที่ของรูปสี่เหลี่ยมเหล่านี้ให้การประมาณพื้นที่ใต้เส้นโค้งที่ดี หรืออีกนัยหนึ่ง เราสามารถพูดได้ว่าเมื่อชิ้นส่วนเข้าใกล้ศูนย์ในความกว้าง คำตอบจะเข้าใกล้คำตอบที่แท้จริง ตอนนี้เราเขียน dx สำหรับ \(\Delta x\) เพื่อหมายความว่าความกว้างเข้าใกล้ศูนย์
มาหาสูตรสำหรับแคลคูลัสเชิงปริพันธ์ที่นี่:
สมมติว่าเราต้องหาพื้นที่ใต้เส้นโค้งระหว่างจุด a และ b: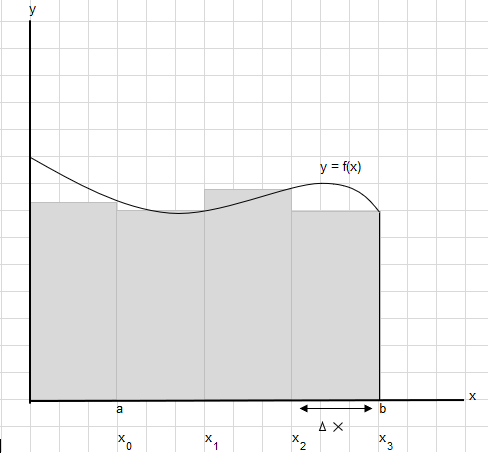
แบ่งพื้นที่ระหว่าง a และ b ออกเป็นส่วนเท่าๆ กัน โดยที่ความกว้างของสี่เหลี่ยมแต่ละอันคือ \(\Delta x\)
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
ผลรวมของพื้นที่ของสี่เหลี่ยมเหล่านี้สามารถเขียนเป็น \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\)
เราสามารถประมาณพื้นที่ได้ดีขึ้นเมื่อ \(\Delta x \) มีขนาดเล็กลงหรืออีกนัยหนึ่งเมื่อจำนวนส่วนเพิ่มขึ้น ดังนั้น \(\Delta x \) จะบางลงและบางลง และ n จะใหญ่ขึ้นเรื่อย ๆ แนวคิดของการประมาณที่ดีขึ้นเมื่อเราใช้ขีดจำกัดเมื่อ n เข้าใกล้อนันต์และ \(\Delta x \) มีขนาดเล็กลงเรื่อยๆ คืออินทิกรัล
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) แทนพื้นที่ภายใต้ f ของ x ระหว่าง x = a และ x = b
การหาอินทิกรัลเป็นสิ่งที่ตรงกันข้ามกับการหา อนุพันธ์
อนุพันธ์ของ x 2 คือ 2x อินทิกรัลของ 2x คือ x 2
\(\int 2x \space dx = x^2 + C\) โดยที่ C เป็นค่าคงที่ เนื่องจากอนุพันธ์ของค่าคงที่คือ 0 ดังนั้น อนุพันธ์ของ x 2 , x 2 +4, x 2 +10, x 2 +99 คือ 2x ดังนั้น อินทิกรัลของ 2x คือ x 2 +C
ลองดู ปริพันธ์ของฟังก์ชันทั่วไป:
| ฟังก์ชั่นทั่วไป | การทำงาน | อินทิกรัล |
| คงที่ | \(\int a \cdot dx\) | \(ax + c\) |
| ตัวแปร | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| สี่เหลี่ยม | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| เลขชี้กำลัง | \(\int e^x \cdot dx\) | \(e^x + c\) |
| ตรีโกณมิติ(x เป็นเรเดียน) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
กฎการรวมทั่วไป:
| กฎ | การทำงาน | อินทิกรัล |
| คูณด้วยค่าคงที่ | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| กฎกำลังไฟฟ้า(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| กฎผลรวม | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| กฎความแตกต่าง | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
คลาสของปริพันธ์
\(\int f(x) \space dx\) แทนอินทิกรัลที่ไม่แน่นอน และ \(\int_a^bf(x) \cdot dx\) แทนอินทิกรัลที่แน่นอน อินทิกรัลที่แน่นอนมีค่าเริ่มต้นและสิ้นสุด ในที่นี้ a และ b เรียกว่าลิมิตหรือขอบเขต อินทิกรัลที่ไม่แน่นอนเป็นรูปแบบทั่วไปของการอินทิเกรตและสามารถตีความได้ว่าเป็นการต่อต้านอนุพันธ์ของฟังก์ชัน
เราหาอินทิกรัลแน่นอนโดยการคำนวณอินทิกรัลไม่จำกัดที่ a และที่ b แล้วลบออก ให้เราเข้าใจสิ่งนี้ด้วยตัวอย่าง:
เรารู้ว่า \(\int 2x \cdot dx = x^2 + C\) ค่าของอินทิกรัลที่แน่นอน \(\int _1^2 2x \cdot dx \) จะเป็นเท่าใด
ที่ x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
ที่ x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
ลบ (4 + C) - (1 + C) = 3
ค่าของ \(\int _1^2 2x \cdot dx \) = 3